Phân tích một vectơ thành hai hay nhiều vectơ cho trước (bài tập + lời giải)

---

Haylamdo sưu tầm bài viết phương pháp giải bài tập Phân tích một vectơ thành hai hay nhiều vectơ cho trước lớp 10 chương trình sách mới hay, chi tiết với bài tập tự luyện đa dạng giúp học sinh ôn tập, biết cách làm bài tập Phân tích một vectơ thành hai hay nhiều vectơ cho trước.

Phân tích một vectơ thành hai hay nhiều vectơ cho trước (bài tập + lời giải)

Phân tích một vectơ thành hai hay nhiều vectơ cho trước

1. Phương pháp giải

- Phân tích một vectơ theo hai vectơ không cùng phương: Cho hai vectơ $\overrightarrow{a}$ và $\overrightarrow{b}$ không cùng phương. Khi đó mọi vectơ $\overrightarrow{x}$ đều phân tích được một cách duy nhất theo hai vectơ $\overrightarrow{a}$ và $\overrightarrow{b}$, nghĩa là có duy nhất cặp số h, k sao cho $\overrightarrow{x}=h\overrightarrow{a}+k\overrightarrow{b}$.

- Sử dụng các quy tắc ba điểm, quy tắc trừ, quy tắc hình bình hành, tính chất về phép toán vectơ, tính chất trung điểm, trọng tâm trong tam giác để biến đổi.

2. Ví dụ minh họa

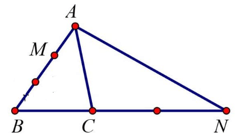
Ví dụ 1. Cho tam giác ABC. Đặt $\overrightarrow{AB}=\overrightarrow{a}$, $\overrightarrow{AC}=\overrightarrow{b}$. M thuộc cạnh AB sao cho AB = 3AM, N thuộc tia BC và CN = 2BC. Phân tích $\overrightarrow{CM}$ qua các vectơ $\overrightarrow{a}$ và $\overrightarrow{b}$.

Hướng dẫn giải:

Theo đề bài: AB = 3AM nên $\overrightarrow{AM}=\frac{1}{3}\overrightarrow{AB}$

Ta có:

$\overrightarrow{CM}=\overrightarrow{CA}+\overrightarrow{AM}=-\overrightarrow{AC}+\frac{1}{3}\overrightarrow{AB}=-\overrightarrow{b}+\frac{1}{3}\overrightarrow{a}$

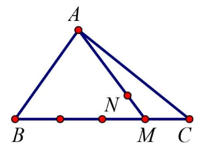
Ví dụ 2. Cho tam giác ABC, trên cạnh BC lấy M sao cho BM = 3CM, trên đoạn AM lấy N sao cho 2AN = 5MN. Phân tích vectơ $\overrightarrow{AM}$ qua các vectơ $\overrightarrow{AB}$ và $\overrightarrow{AC}$.

Hướng dẫn giải:

Theo đề bài ta có: $\overrightarrow{BM}=\frac{3}{4}\overrightarrow{BC}$

Ta có:

$\overrightarrow{AM}=\overrightarrow{AB}+\overrightarrow{BM}=\overrightarrow{AB}+\frac{3}{4}\overrightarrow{BC}=\overrightarrow{AB}+\frac{3}{4}\left(\overrightarrow{AC}-\overrightarrow{AB}\right)=\frac{1}{4}\overrightarrow{AB}+\frac{3}{4}\overrightarrow{AC}$

3. Bài tập tự luyện.

Bài 1. Cho tam giác ABC. Đặt $\overrightarrow{AB}=\overrightarrow{a}$, $\overrightarrow{AC}=\overrightarrow{b}$. M thuộc cạnh AB sao cho AB = 3AM, N thuộc tia BC và CN = 2BC. Phân tích $\overrightarrow{AN}$ qua các vectơ $\overrightarrow{a}$ và $\overrightarrow{b}$ ta được biểu thức là:

A. $2\overrightarrow{a}+3\overrightarrow{b}$;

B. $-2\overrightarrow{a}+3\overrightarrow{b}$;

C. $2\overrightarrow{a}-3\overrightarrow{b}$;

D. $2\overrightarrow{a}+\overrightarrow{b}$.

Bài 2. Cho tam giác ABC. Đặt $\overrightarrow{AB}=\overrightarrow{a}$, $\overrightarrow{AC}=\overrightarrow{b}$. M thuộc cạnh AB sao cho AB = 3AM, N thuộc tia BC và CN = 2BC. Phân tích $\overrightarrow{MN}$ qua các vectơ $\overrightarrow{a}$ và $\overrightarrow{b}$  ta được biểu thức là:

A. $-\frac{7}{3}\overrightarrow{a}+3\overrightarrow{b}$;

B. $-\frac{1}{3}\overrightarrow{a}+3\overrightarrow{b}$;

C. $-\frac{2}{3}\overrightarrow{a}+3\overrightarrow{b}$;

D. $-\frac{5}{3}\overrightarrow{a}+3\overrightarrow{b}$.

Bài 3. Cho tam giác ABC, trên cạnh BC lấy M sao cho BM = 3CM, trên đoạn AM lấy N sao cho 2AN = 5MN. Phân tích vectơ $\overrightarrow{BN}$ qua các vectơ $\overrightarrow{AB}$ và $\overrightarrow{AC}$.

A. $\overrightarrow{BN}=\frac{23}{28}\overrightarrow{AB}+\frac{15}{28}\overrightarrow{AC}$;

B. $\overrightarrow{BN}=-\frac{23}{28}\overrightarrow{AB}-\frac{15}{28}\overrightarrow{AC}$;

C. $\overrightarrow{BN}=-\frac{23}{28}\overrightarrow{AB}+\frac{15}{28}\overrightarrow{AC}$;

D. $\overrightarrow{BN}=\frac{23}{28}\overrightarrow{AB}-\frac{15}{28}\overrightarrow{AC}$.

Bài 4. Cho tam giác ABC, G là trọng tâm của tam giác ABC. Phân tích vectơ $\overrightarrow{GC}$ qua các vectơ $\overrightarrow{GA}$ và $\overrightarrow{GB}$.

A. $\overrightarrow{GC}=\overrightarrow{GA}+\overrightarrow{GB}$;

B. $\overrightarrow{GC}=\overrightarrow{-GA}-\overrightarrow{GB}$;

C. $\overrightarrow{GC}=\overrightarrow{-GA}+\overrightarrow{GB}$;

D. $\overrightarrow{GC}=\overrightarrow{GA}-\overrightarrow{GB}$.

Bài 5. Cho tam giác ABC, trên cạnh BC lấy M sao cho BM = 3CM, trên đoạn AM lấy N sao cho 2AN = 5MN. G là trọng tâm của tam giác ABC. Phân tích vectơ $\overrightarrow{MN}$ qua các vectơ $\overrightarrow{GA}$ và $\overrightarrow{GB}$.

A. $\overrightarrow{MN}=\frac{1}{2}\overrightarrow{GA}+\frac{1}{7}\overrightarrow{GB}$;

B. $\overrightarrow{MN}=\frac{1}{7}\overrightarrow{GA}+\frac{1}{7}\overrightarrow{GB}$;

C. $\overrightarrow{MN}=\frac{2}{7}\overrightarrow{GA}-\frac{1}{7}\overrightarrow{GB}$;

D. $\overrightarrow{MN}=\frac{1}{2}\overrightarrow{GA}+\frac{2}{7}\overrightarrow{GB}$.

Bài 6. Cho hình bình hành ABCD. Gọi M, N lần lượt là hai điểm nằm trên hai cạnh AB và CD sao cho AB = 3AM, CD = 2CN. Biểu diễn vectơ $\overrightarrow{AN}$ qua các vectơ $\overrightarrow{AB}$ và $\overrightarrow{AC}$.

A. $\overrightarrow{AN}=-\overrightarrow{AC}+\frac{1}{2}\overrightarrow{AB}$;

B. $\overrightarrow{AN}=\overrightarrow{AC}+\frac{1}{2}\overrightarrow{AB}$;

C. $\overrightarrow{AN}=-\overrightarrow{AC}-\frac{1}{2}\overrightarrow{AB}$;

D. $\overrightarrow{AN}=\overrightarrow{AC}-\frac{1}{2}\overrightarrow{AB}$.

Bài 7. Cho hình bình hành ABCD. Gọi M, N lần lượt là hai điểm nằm trên hai cạnh AB và CD sao cho AB = 3AM, CD = 2CN và G là trọng tâm tam giác MNB. Phân tích vectơ $\overrightarrow{MN}$ qua các vectơ $\overrightarrow{AB}$ và $\overrightarrow{AC}$.

A. $\overrightarrow{MN}=\frac{5}{6}\overrightarrow{AB}-2\overrightarrow{AC}$;

B. $\overrightarrow{MN}=\frac{5}{6}\overrightarrow{AB}+\overrightarrow{AC}$;

C. $\overrightarrow{MN}=-\frac{5}{6}\overrightarrow{AB}+\overrightarrow{AC}$;

D. $\overrightarrow{MN}=-\frac{5}{6}\overrightarrow{AB}-\overrightarrow{AC}$.

Bài 8. Cho hình bình hành ABCD. Gọi M, N lần lượt là hai điểm nằm trên hai cạnh AB và CD sao cho AB = 3AM, CD = 2CN và G là trọng tâm tam giác MNB. Phân tích vectơ $\overrightarrow{AG}$ qua các vectơ $\overrightarrow{AB}$ và $\overrightarrow{AC}$ ta được $\overrightarrow{AG}=\frac{a}{b}\overrightarrow{AB}+\frac{c}{d}\overrightarrow{AC}$ với $\frac{a}{b}$ và $\frac{c}{d}$ là các phân số tối giản. Khi đó ta có: $\frac{a}{b}+\frac{c}{d}=?$

A. $\frac{11}{18}$;

B. $\frac{5}{18}$;

C. $\frac{1}{3}$;

D. $-\frac{1}{18}$.

Bài 9. Cho AK và BM là hai trung tuyến của tam giác ABC. Phân tích vectơ $\overrightarrow{AB}$ theo hai vectơ $\overrightarrow{AK}=\overrightarrow{u}$ và $\overrightarrow{BM}=\overrightarrow{v}$ ta được biểu thức là:

A. $\frac{2}{3}\overrightarrow{u}-\frac{1}{2}\overrightarrow{v}$;

B. $\frac{2}{3}\overrightarrow{u}+\frac{1}{2}\overrightarrow{v}$;

C. $\frac{2}{3}\overrightarrow{u}-\frac{2}{3}\overrightarrow{v}$;

D. $\frac{2}{3}\overrightarrow{u}+\frac{2}{3}\overrightarrow{v}$.

Bài 10. Cho tam giác ABC. Gọi I là điểm trên cạnh BC sao cho $2\overrightarrow{IC}=3\overrightarrow{BI}$. Phân tích vectơ $\overrightarrow{AI}$ theo hai vectơ $\overrightarrow{AB}$ và $\overrightarrow{AC}$.

A. $\frac{3}{5}\overrightarrow{AB}+\frac{1}{5}\overrightarrow{AC}$;

B. $\frac{3}{5}\overrightarrow{AB}-\frac{1}{5}\overrightarrow{AC}$;

C. $\frac{3}{5}\overrightarrow{AB}+\frac{2}{5}\overrightarrow{AC}$;

D. $\frac{3}{5}\overrightarrow{AB}-\frac{2}{5}\overrightarrow{AC}$.