Xác định hiệu của hai tập hợp, phần bù của tập con (bài tập + lời giải)

---

Haylamdo sưu tầm bài viết phương pháp giải bài tập Xác định hiệu của hai tập hợp, phần bù của tập con lớp 10 chương trình sách mới hay, chi tiết với bài tập tự luyện đa dạng giúp học sinh ôn tập, biết cách làm bài tập Xác định hiệu của hai tập hợp, phần bù của tập con.

Xác định hiệu của hai tập hợp, phần bù của tập con (bài tập + lời giải)

1. Phương pháp giải

Cho hai tập hợp A và B.

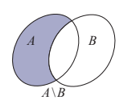
Tập hợp các phần tử thuộc A nhưng không thuộc B gọi là hiệu của A và B, kí hiệu là A \ B.

A \ B = {x | x ∈ A và x ∉ B}.

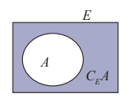
Nếu A là tập con của E (A ⊂ E) thì E \ A gọi là phần bù của A trong E, kí hiệu là C_EA.

- Để xác định hiệu của hai tập hợp ta có thể làm một số cách sau:

+ Biểu diễn các tập hợp lên trục số rồi dùng định nghĩa các phép toán hiệu, phần bù để xác định các phần tử của tập hợp.

+ Liệt kê các phần tử của mỗi tập hợp rồi dùng định nghĩa các phép toán hiệu, phần bù để xác định các phần tử của tập hợp.

2. Ví dụ minh họa

Ví dụ 1: Cho hai tập hợp A = (0; 3), B = (2; 4).

Xác định A \ B và C_ℝA.

Hướng dẫn giải:

– Biểu diễn tập hợp A trên trục số ta có:

– Biểu diễn tập hợp B trên trục số ta có:

Vì hiệu của tập hợp A và B là các phần tử thuộc A nhưng không thuộc B.

Mà nhìn vào trục số trên ta thấy nửa khoảng (0; 2] thuộc tập hợp A, không thuộc tập hợp B do đó hiệu của A và B gồm các phần tử nằm trong nửa khoảng (0; 2].

Vậy A \ B = (0; 2].

+ Ta có: C_ℝA = ℝ \ A.

Ta có ℝ \ A là tập hợp tất cả các phần tử thuộc ℝ mà không thuộc tập hợp A.

Vậy C_ℝA = ℝ \ A = (–∞; 0] ∪ [3; +∞).

Ví dụ 2: Cho các tập hợp:

A = {x ∈ ℤ | –3 ≤ x ≤ 4};

B = {x ∈ ℤ | –1 ≤ x ≤ 1}.

Xác định A \ B và C_AB.

Hướng dẫn giải:

Ta có:

+ Các phần tử của tập hợp A là –3; –2; –1; 0; 1; 2; 3; 4.

Do đó, A = {–3; –2; –1; 0; 1; 2; 3; 4}.

+ Các phần tử của tập hợp B là –1; 0; 1.

Do đó, B = {–1; 0; 1}.

Các phần tử thuộc A mà không thuộc B là –3; –2; 2; 3; 4.

Vậy A \ B = {–3; –2; 2; 3; 4}.

Ta thấy B là tập con của A (do tất cả các phần tử của B đều thuộc A).

Vậy C_AB = A \ B = {–3; –2; 2; 3; 4}.

3. Bài tập tự luyện

Bài 1: Cho các tập hợp:

A = {x ∈ ℤ | –1 < x < 6}; B = {x ∈ ℤ | 0 ≤ x ≤ 1}.

Xác định A \ B. Câu nào sau đây đúng?

A. A \ B = {2; 3; 4};

B. A \ B = {2; 3; 4; 5};

C. A \ B = {2; 3};

D. A \ B = {3; 4; 5}.

Bài 2: Cho tập hợp K = [1 ; 7) \ (– 3 ; 5). Khẳng định nào sau đây đúng ?

A. K = [1; 7);

B. K = (– 3; 7);

C. K = [1; 5);

D. K = [5; 7).

Bài 3: Cho các tập hợp:

A = {x ∈ ℤ | –6 ≤ x ≤ 0}; B = {x ∈ ℤ | –1 ≤ x ≤ 0}.

Xác định C_AB. Câu nào sau đây đúng?

A. C_AB = {–6; –5; –4; –3; –2};

B. C_AB = {–5; –4; –3; –2};

C. C_AB = {–6; –5; –4; –3};

D. C_AB = {–6; –5; –4; –3; –2; –1}.

Bài 4: Cho các tập hợp:

A = {x ∈ ℤ | –1 ≤ x ≤ 2}; B = {x ∈ ℤ | –4 ≤ x ≤ 4}.

Xác định C_BA. Câu nào sau đây đúng?

A. C_BA = {–3; –2; 3; 4};

B. C_BA = {–4; –3; –2; 3};

C. C_BA = {–4; –3; –2; 3; 4};

D. C_BA = {–4; –3; –2; –1; 3; 4}.

Bài 5: Cho các tập hợp:

A = {x ∈ ℤ | –2 < x ≤ 4}; B = {x ∈ ℤ | 1 ≤ x ≤ 7}.

Xác định tập hợp X = (A \ B) ∪ (B \ A). Câu nào sau đây đúng?

A. X = {0; 5; 6; 7};

B. X = {–1; 0; 5; 6};

C. X = {–1; 0; 5};

D. X = {–1; 0; 5; 6; 7}.

Bài 6: Cho các tập hợp:

A = {x ∈ ℤ | –3 < x < 3}; B = {x ∈ ℤ | 0 ≤ x ≤ 5}.

Xác định tập hợp M = (A \ B) ∩ (B \ A). Câu nào sau đây đúng?

A. M = {–2; –1};

B. M = ∅;

C. M = {3; 4; 5};

D. M = {–2; –1; 3; 4; 5}.

Bài 7: Cho các tập hợp:

A = {x ∈ ℤ | –4 ≤ x ≤ 5}; B = {x ∈ ℤ | –2 ≤ x ≤ 6}; C = {x ∈ ℤ | 0 ≤ x ≤ 1}.

Xác định tập hợp X = (A ∩ B) \ C. Câu nào sau đây đúng?

A. X = {–1; 2; 3; 4; 5};

B. X = {2; 3; 4; 5};

C. X = {–2; –1; 2; 3; 4; 5};

D. X = {–2; –1; 2; 3; 4}.

Bài 8: Cho các tập hợp:

A = {x ∈ ℤ | 0 ≤ x ≤ 6}; B = {x ∈ ℤ | 4 < x < 9}; C = {x ∈ ℤ | 2 ≤ x ≤ 3}.

Xác định tập hợp X = (A \ B) \ C. Câu nào sau đây đúng?

A. X = {0; 1; 4};

B. X = {0; 1};

C. X = {1; 4};

D. X = ∅.

Bài 9: Cho các tập hợp:

A = {x ∈ ℤ | –2 < x ≤ 2}; B = {x ∈ ℤ | 3 ≤ x ≤ 5}; C = {x ∈ ℤ | 0 ≤ x ≤ 3}.

Xác định tập hợp X = (A ∪ B) \ C. Câu nào sau đây đúng?

A. X = {–1; 4};

B. X = {–1; 4; 5};

C. X = {–1; 3; 4; 5};

D. X = ∅.

Bài 10: Cho hai nửa khoảng M = (0; 2], N = [1; 4). Tìm E = C_ℝ(M ∩ N).

A. E = (0; 4);

B. E = [1; 2];

C. E = (– ∞; 1) ∪ (2; +∞);

D. E = (– ∞; 0] ∪ [4; +∞).