Xác định hợp và giao của hai tập hợp (bài tập + lời giải)
Haylamdo sưu tầm bài viết phương pháp giải bài tập Xác định hợp và giao của hai tập hợp lớp 10 chương trình sách mới hay, chi tiết với bài tập tự luyện đa dạng giúp học sinh ôn tập, biết cách làm bài tập Xác định hợp và giao của hai tập hợp.
Xác định hợp và giao của hai tập hợp (bài tập + lời giải)
1. Phương pháp giải
1.1. Hợp của hai tập hợp:
Cho hai tập hợp A và B.
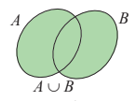
Tập hợp các phần tử thuộc A hoặc thuộc B được gọi là hợp của hai tập hợp A và B, kí hiệu là A ∪ B.
A ∪ B = {x | x ∈ A hoặc x ∈ B}.
Để xác định hợp của hai tập hợp A và B, ta làm như sau:
Liệt kê các phần tử của hai tập hợp, những phần tử thuộc tập hợp này hoặc tập hợp kia là hợp của hai tập hợp đó.
* Đối với các tập hợp được cho dưới dạng một đoạn, khoảng, nửa khoảng, ta có thể xác định hợp của hai tập hợp như sau:
Cách 1:
+ Bước 1. Biểu diễn A, Biểu diễn B trên cùng 1 trục số. Lưu ý không gạch chéo mà tô đậm miền của A và miền của B.
+ Bước 2. Lấy phần tô đậm.
+ Bước 3. Kiểm tra các điểm đặc biệt để tránh nhầm lẫn.
Cách 2:
+ Biểu diễn tập hợp A trên trục số, gạch chéo phần không thuộc A.
+ Làm tương tự đối với tập hợp B trên một trục số khác.
+ Phần không gạch chéo trên hình là A ∪ B.
1.2 Giao của hai tập hợp:
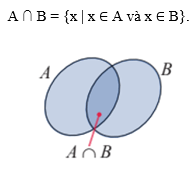
Tập hợp các phần tử thuộc cả hai tập hợp A và B được gọi là giao của hai tập hợp A và B, kí hiệu là A ∩ B.
Để xác định giao của hai tập hợp A và B, ta làm như sau:
Liệt kê các phần tử của hai tập hợp, những phần tử thuộc cả hai tập hợp là giao của hai tập hợp đó.
* Đối với các tập hợp được cho dưới dạng một đoạn, khoảng, nửa khoảng, ta có thể xác định giao của hai tập hợp như sau:
+ Bước 1. Biểu diễn A, Biểu diễn B trên cùng 1 trục số.
+ Bước 2. Lấy phần không bị gạch chéo.
+ Bước 3. Kiểm tra các điểm đặc biệt để tránh nhầm lẫn.
Nhận xét:
√ Nếu A và B là hai tập hợp hữu hạn thì n(A ∪ B) = n(A) + n(B) – n(A ∩ B).
√ Nếu A và B không có phần tử chung, tức A ∩ B = ∅, thì n(A∪ B) = n(A) + n(B).
2. Ví dụ minh họa
Ví dụ 1: Xác định tập hợp (0; 3) ∪ (–3; 2).
Hướng dẫn giải:
Xét tập hợp A = (0; 3)
+ Ta dùng kí hiệu khoảng để biểu diễn tập hợp trên.
+ Ta chỉ nhận các giá trị từ 0 đến 3 và gạch bỏ phần bé hơn 0 và lớn hơn 3.
Tập hợp A được biểu diễn trên trục số như sau:
Tương tự, ta biểu diễn tập hợp B trên trục số như sau:
Do đó, phần hợp của hai tập hợp A và B là tất cả những phần không gạch chéo trong hai hình vẽ trên:
Vậy (0; 3) ∪ (–3; 2) = (–3; 3).
Ví dụ 2: Cho hai tập hợp A = {x ∈ ℤ |– 2 < x < 3} và B = {x ∈ ℤ | 1 ≤ x ≤ 3}.
Xác định tập hợp A ∩ B.
Hướng dẫn giải:
Ta có:
+ Tập hợp A = {x ∈ ℤ |– 2 < x < 3} là tập hợp các số nguyên lớn hơn – 2 và nhỏ hơn 3. Do đó ta viết tập hợp A dưới dạng liệt kê các phần tử như sau:
A = {–1; 0; 1; 2}.
+ Tập hợp B = {x ∈ ℤ | 1 ≤ x ≤ 3}là tập hợp các số nguyên lớn hơn hoặc bằng 1 và nhỏ hơn hoặc bằng 3. Do đó ta viết tập hợp B dưới dạng liệt kê các phần tử như sau:
B = {1; 2; 3}.
Giao của hai tập hợp A và B là tập hợp những phần tử vừa thuộc A vừa thuộc B nên ta có: A ∩ B = {1; 2}.
3. Bài tập tự luyện
Bài 1: Cho các tập hợp:
A = {x ∈ ℤ | – 5 < x < 6};
B = {x ∈ ℤ | 1 < x < 6}.
Xác định tập hợp X = A ∩ B.
A. X = {2; 3; 4};
B. X = {2; 3; 4; 5};
C. X = {3; 4; 5};
D. X = {1; 2; 3; 4}.
Bài 2: Cho hai tập hợp:
X = {x ∈ ℕ | 0 ≤ x ≤ 5}
Y là tập hợp các ước số tự nhiên của 15.
X ∩ Y là tập hợp nào dưới đây?
A. A = {1; 2; 3; 4; 5};
B. B = {1; 2; 3};
C. C = {3; 4; 5};
D. D = {1; 3; 5}.
Bài 3: Xác định tập hợp A = (1; 4) ∪ (3; 5).
A. A = (1; 5);
B. B = (2; 4);
C. C = (1; 4);
D. D = (2; 5).
Bài 4: Cho hai tập hợp sau:
M là tập hợp các số tự nhiên chẵn lớn hơn 0 và bé hơn 10.
N là tập hợp ba số nguyên tố đầu tiên.
M ∪ N là tập hợp nào dưới đây?
A. A = {2; 4; 6; 8};
B. B = {1; 2; 3};
C. C = {0; 2; 4; 6; 8; 10};
D. D = {2; 3; 4; 5; 6; 8}.
Bài 5: Cho các tập hợp:
A = {x ∈ ℤ | 1 ≤ x ≤ 4};
B = {x ∈ ℤ | 2 < x < 7}.
Xác định tập hợp X = A ∩ B.
A. X = {1; 2; 3; 4};
B. X = {3; 4; 5; 6};
C. X = {3; 4};
D. X = {4; 5}.
Bài 6: Cho các tập hợp:
A = {x ∈ ℤ | 5 < x < 8};
B = {x ∈ ℤ | 8 < x < 11}.
Xác định tập hợp X = A ∩ B.
A. X = {6; 7};
B. X = {8; 9};
C. X = {9; 10};
D. X = ∅.
Bài 7: Cho hai tập hợp:
A = {x ∈ ℤ | x(x2 – 1) = 0}
B = {x ∈ ℕ | 2 < x < 5}
Câu nào sau đây đúng?
A. A ∪ B = {1; 2; 3; 4};
B. A ∪ B = {–1; 0; 1; 3; 4};
C. A ∪ B = {–1; 0; 1; 2; 3}
D. A ∪ B = {2; 3; 4; 5}.
Bài 8: Cho tập hợp H = [1; 7] ∩ (– 3; 5). Đáp án nào sau đây là đúng.
A. H = [1; 7];
B. H = (– 3; 5);
C. H = [1; 5] ;
D. H = [1; 5).
Bài 9: Cho hai tập hợp:
A = {x ∈ ℤ | x2 – 9 = 0}
B = {x ∈ ℤ | x2 + 6x + 5 = 0}
Câu nào sau đây đúng?
A. A ∪ B = {–3; 3};
B. A ∪ B = {–5; –1};
C. A ∪ B = {–5; –3; –1};
D. A ∪ B = {–5; –3; –1; 3}.
Bài 10: Cho tập hợp H = [1; 7) ∪ (– 3; 5). Đáp án nào sau đây là đúng.
A. H = [1; 7];
B. H = (– 3; 7);
C. H = [1; 5] ;
D. H = [1; 5).