Tổng hợp lý thuyết Chương 2: Tổ hợp - Xác suất hay, chi tiết nhất - Toán lớp 11

Tổng hợp lý thuyết Chương 2: Tổ hợp - Xác suất hay, chi tiết nhất

Tài liệu Tổng hợp lý thuyết Chương 2: Tổ hợp - Xác suất hay, chi tiết nhất Toán lớp 11 sẽ tóm tắt kiến thức trọng tâm về Chương 2: Tổ hợp - Xác suất từ đó giúp học sinh ôn tập để nắm vứng kiến thức môn Toán lớp 11.

• Lý thuyết Quy tắc đếm
• Lý thuyết Hoán vị - Chỉnh hợp - Tổ hợp
• Lý thuyết Nhị thức Niu-tơn
• Lý thuyết Phép thử và biến cố
• Lý thuyết Xác suất của biến cố
• Lý thuyết Tổng hợp chương Tổ hợp - Xác suất

Lý thuyết Quy tắc đếm

I. TÓM TẮT LÝ THUYẾT

1. Quy tắc cộng

- Quy tắc: Một công việc được hoàn thành bởi một trong hai hành động. Nếu hành động này có m cách thực hiện, hành động kia có n cách thực hiện không trùng với bất kì cách nào của hành động thứ nhất thì công việc đó có m+n cách thực hiện.

- Quy tắc cộng có thể mở rộng cho nhiều hành động.

2. Quy tắc nhân

- Quy tắc: Một công việc được hoàn thành bởi hai hành động liên tiếp. Nếu có m cách thực hiện hành động thứ nhất và ứng với mỗi cách đó có n cách thực hiện hành động thứ hai thì có m.n cách hoàn thành công việc.

- Quy tắc nhân có thể mở rộng cho nhiều hành động.

Lý thuyết Hoán vị - Chỉnh hợp - Tổ hợp

I. TÓM TẮT LÝ THUYẾT

1. Hoán vị

a) Định nghĩa:

- Cho tập hợp A gồm n phần tử (n ≥ 1).

    Mỗi kết quả của sự sắp xếp thứ tự n phần tử của tập hợp A được gọi là một hoán vị của n phần tử.

- Lưu ý: Hai hoán vị của n phần tử chỉ khác nhau ở thứ tự sắp xếp.

b) Số các hoán vị:

- Kí hiệu P_n là số các hoán vị của n phần tử.

- Định lý:

    P_n = n(n – 1)…2.1 = n!

2. Chỉnh hợp

a) Định nghĩa:

- Cho tập hợp A gồm n phần tử (n ≥ 1).

Kết quả của việc lấy k phần tử khác nhau từ n phần tử của tập hợp A và sắp xếp chúng theo một thứ tự nào đó được gọi là một chỉnh hợp chập k của n phần tử đã cho.

b) Số các chỉnh hợp:

- Kí hiệu: A_n^k là số các chỉnh hợp chập k của n phần tử (1 ≤ k ≤ n).

- Định lý:

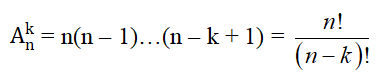
- Lưu ý: Mỗi hoán vị của n phần tử cũng chính là một chỉnh hợp chập n của n phần tử đó. Vì vậy, ta có: P_n = A_nⁿ

3. Tổ hợp

a) Định nghĩa:

- Giả sử A có n phần tử (n ≥ 1). Mỗi tập hợp gồm k phần tử của A được gọi là một tổ hợp chập k của n phần tử đã cho. (1 ≤ k ≤ n).

- Quy ước: Tổ hợp chập 0 của n phần tử là tập rỗng.

b) Số các tổ hợp:

- Kí hiệu C_n^k là số các tổ hợp chập k của n phần tử (0 ≤ k ≤ n).

- Định lý:

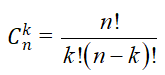
c) Tính chất của các số C_n^k

- Tính chất 1:

    C_n^k = C_n^{n - k} (0 ≤ k ≤ n)

- Tính chất 2:

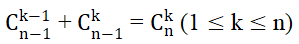
Lý thuyết Nhị thức Niu-tơn

I. TÓM TẮT LÝ THUYẾT

1. Công thức nhị thức Niu-tơn

    (a + b)ⁿ = C_n⁰aⁿ + C_n¹a^{n - 1}b + … + C_n^ka^{n - k}b^k + … + C_n^n-1ab^n-1 + C_nⁿbⁿ (1)

2. Hệ quả

- Với a = b = 1, ta có: 2ⁿ = C_n⁰ + C_n¹ + … + C_nⁿ.

- Với a = 1; b = –1, ta có: 0 = C_n⁰ – C_n¹ + … + (–1)^kC_n^k + … + (–1)C_nⁿ.

3. Chú ý:

Trong biểu thức ở vế phải của công thức (1):

-Số các hạng tử là n + 1;

- Các hạng tử có số mũ của a giảm dần từ n đến 0, số mũ của b tăng dần từ 0 đến n, nhưng tổng các số mũ của a và b trong mỗi hạng tử luôn bằng n (quy ước a⁰ = b⁰ = 1);

- Các hệ số của mỗi hạng tử cách đều hai hạng tử đầu và cuối thì bằng nhau.