Tổng hợp lý thuyết Chương 1: Hàm số lượng giác - phương trình lượng giác hay, chi tiết nhất - Toán lớp 11

---

Tổng hợp lý thuyết Chương 1: Hàm số lượng giác - phương trình lượng giác hay, chi tiết nhất

Tài liệu Tổng hợp lý thuyết Chương 1: Hàm số lượng giác - phương trình lượng giác hay, chi tiết nhất Toán lớp 11 sẽ tóm tắt kiến thức trọng tâm về Chương 1: Hàm số lượng giác - phương trình lượng giác từ đó giúp học sinh ôn tập để nắm vứng kiến thức môn Toán lớp 11.

• Lý thuyết Hàm số lượng giác
• Lý thuyết Phương trình lượng giác cơ bản
• Lý thuyết Một số phương trình lượng giác thường gặp
• Lý thuyết Tổng hợp chương Hàm số lượng giác - phương trình lượng giác

Lý thuyết Hàm số lượng giác

I. TÓM TẮT LÝ THUYẾT:

1. Hàm số sin và hàm số cosin

a) Hàm số sin

- Định nghĩa:

    Quy tắc đặt tương ứng mỗi số thực x đối với số thực sin x

    sin: R → R

    x → y = sin x

được gọi là hàm số sin, kí hiệu là: y = sinx.

- Tập xác định của hàm số sin là R.

- Là hàm số lẻ.

b) Hàm số côsin

- Định nghĩa:

Quy tắc đặt tương ứng mỗi số thực x đối với số thực cos x

cos: R → R

x → y = cos x

được gọi là hàm số cosin, kí hiệu là: y = cos x.

- Tập xác định của hàm số cosin là R.

- Là hàm số chẵn.

2. Hàm số tang và hàm số cotang

a) Hàm số tang

- Định nghĩa: Hàm số tang là hàm số được xác định bới công thức: 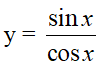(cos x ≠ 0)

- Kí hiệu là y = tan x

- Tập xác định của hàm số y = tan x là D = R\{π/2 + kπ, k ∈ Z}.

- Là hàm số lẻ.

b) Hàm số cotang

- Định nghĩa:

    Hàm số cotang là hàm số được xác định bới công thức: 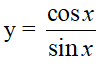(sin x ≠ 0)

- Kí hiệu là y = cot x

- Tập xác định của hàm số y = cot x là D = R\{kπ, k ∈ Z}.

- Là hàm số lẻ.

3. Tính tuần hoàn của hàm lượng giác

- Các hàm số y = sin x và y = cos x là những hàm số tuần hoàn với chu kì 2π.

- Các hàm số y = tan x và y = cot x là những hàm số tuần hoàn với chu kì π.

4. Sự biến thiên và đồ thị của hàm số lượng giác

a) Hàm số y = sin x

- Sự biến thiên và đồ thị hàm số y = sin x trên đoạn [0; π]:

    Hàm số y = sin x đồng biến trên [0; π/2] và nghịch biến trên [π/2; π]

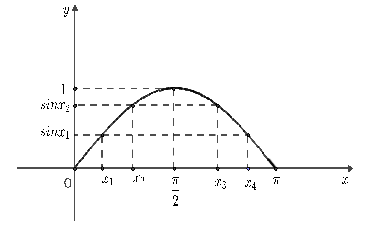
- Lưu ý: Vì y = sin x là hàm số lẻ nên lấy đối xứng đồ thị hàm số trên đoạn [0; π] qua gốc tọa độ O, ta được đồ thị hàm số trên đoạn [–π; 0]

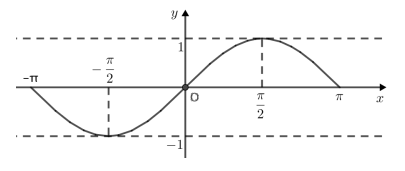
- Đồ thị hàm số y = sin x trên R: Tịnh tiến liên tiếp đồ thị hàm số trên đoạn [–π; π] theo các vecto v→ = (2π; 0) và –v→ = (–2π; 0)

- Tập giá trị của hàm số y = sin x là [–1; 1]

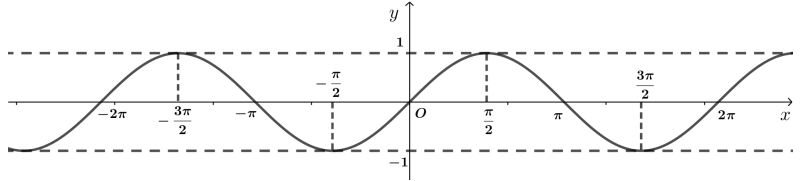
b) Hàm số y = cos x

- Bằng cách tịnh tiến đồ thị hàm số y = sin x theo vectơ u→ = (-π/2; 0), ta được đồ thị của hàm số y = cos x.

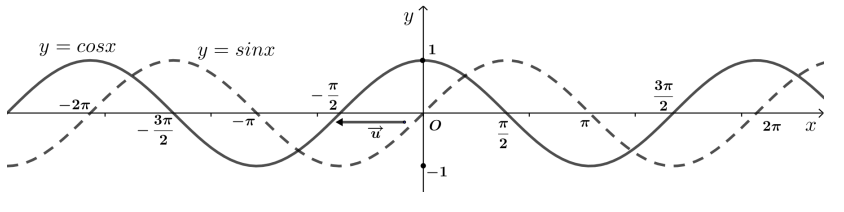
- Hàm số y = cos x đồng biến trên [–π; 0] và nghịch biến trên [0; π]

- Tập giá trị của hàm số y = cos x là [–1; 1]

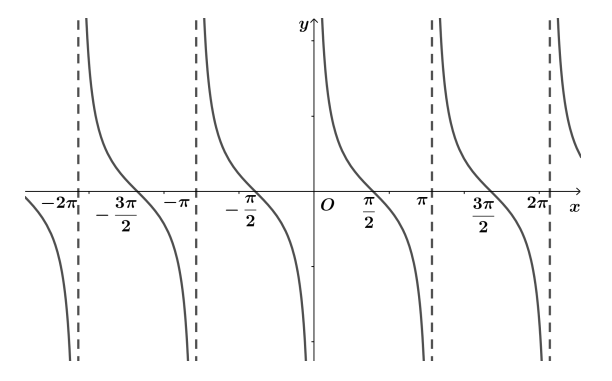
c) Hàm số y = tan x

- Hàm số y = tan x đồng biến trên [0; π/2 )

- Đồ thị hàm số có tâm đối xứng là gốc tọa độ O

=> Lấy đối xứng qua tâm O đồ thị hàm số y = tan x trên [0; π/2 ), ta được đồ thị hàm số y = tan x trên (–π/2; 0]

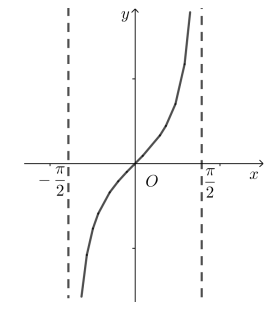
- Tịnh tiến đồ thị hàm số trên khoảng (–π/2 ; π/2) songsong với trục hoành từng đoạn có độ dài π, ta được đồ thị hàm số y = tan x trên D.

Tập giá trị của hàm số y = tan x là khoảng (–∞; +∞)

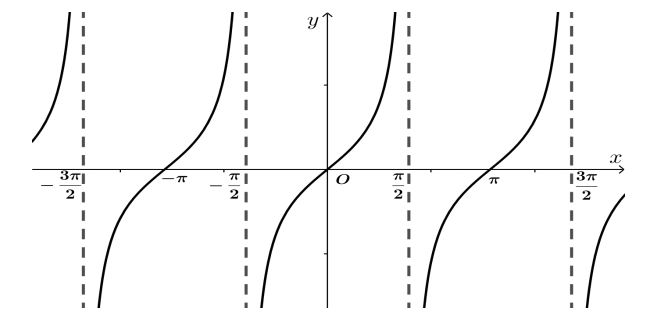
d) Hàm số y = cot x

- Hàm số y = cot x nghịch biến trên khoảng (0; π)

- Tịnh tiến đồ thị hàm số trên khoảng (0; π) song song với trục hoành từng đoạn có độ dài π, ta được đồ thị hàm số y = cot x trên D.

- Tập giá trị của hàm số y = cot x là khoảng (–∞; +∞)

Lý thuyết Phương trình lượng giác cơ bản

I. TÓM TẮT LÝ THUYẾT

1. Phương trình sin x = a (1)

- Trường hợp |a| > 1: Phương trình (1) vô nghiệm

- Trường hợp |a| ≤ 1: Phương trình (1) có các nghiệm là

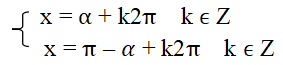
+ Nếu số thực α thoả mãn điều kiện

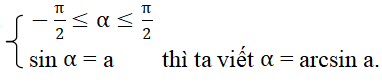
- Lưu ý:

+ Phương trình sin x = sin α, với α là một số cho trước, có các nghiệm là:

    x = α + k2π    k ∈ Z và x = π – α + k2π    k ∈ Z

Tổng quát: sin f(x) = sin g(x)

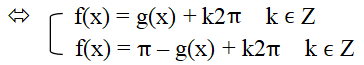
+ sin x = sin β°

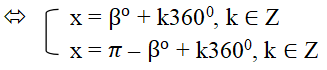
+ Các trường hợp đặc biệt:

    a = 1: Phương trình sin x = 1 có các nghiệm là: x = π/2 + k2π    k ∈ Z.

    a = –1: Phương trình sin x = –1 có các nghiệm là: x = -π/2 + k2π    k ∈ Z.

    a = 0: Phương trình sin x = 0 có các nghiệm là: x = x = kπ    k ∈ Z.

2. Phương trình cos x = a (2)

- Trường hợp |a| > 1: Phương trình (2) vô nghiệm

- Trường hợp |a| ≤ 1: Phương trình (2) có các nghiệm là

    x = ±α + k2π, k ∈ Z.

+ Nếu số thực α thoả mãn điều kiện:

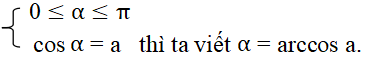
- Lưu ý:

+ Phương trình cos x = cosα, với α là một số cho trước, có các nghiệm là:

    x = ±α + k2π, k ∈ Z.

Tổng quát: cos f(x) = cos g(x) ⇔ f(x) = x = ±g(x) + k2π, k ∈ Z.

+ cos x = cos β° ⇔ x = ±β° + 360°, k ∈ Z.

+ Các trường hợp đặc biệt:

    a = 1: Phương trình cos x = 1 có các nghiệm là: x = k2π, k ∈ Z

    a = –1: Phương trình cos x = –1 có các nghiệm là: x = π + k2π, k ∈ Z

    a = 0: Phương trình cos x = 0 có các nghiệm là: x = π/2 + kπ, k ∈ Z.

3. Phương trình tan x = a (3)

- Điều kiện của phương trình là x ≠ π/2 + kπ, k ∈ Z.

- Nghiệm của phương trình tan x = a là:

    x = arctan α + kπ, k ∈ Z.

- Lưu ý:

+ Phương trình tan x = tan α, với α là một số cho trước, có các nghiệm là:

    x = α + kπ, k ∈ Z.

Tổng quát: tan f(x) = tan g(x) ⇒ f(x) = g(x) + kπ, k ∈ Z.

+ tan x = tan β° ⇔ x = β° + k180°, k ∈ Z.

4. Phương trình cot x = a (4)

- Điều kiện của phương trình là x ≠ kπ, k ∈ Z.

- Nghiệm của phương trình cot x = a là:

    x = arccot α + kπ, k ∈ Z.

- Lưu ý:

+ Phương trình cot x = cot α, với α là một số cho trước, có các nghiệm là:

    x = α + kπ, k ∈ Z.

Tổng quát: cot f(x) = cot g(x) ⇒ f(x) = g(x) + kπ, k ∈ Z.

+ Phương trình cot x = cot β° có các nghiệm là x = β° + k180° , k ∈ Z.

Lý thuyết Một số phương trình lượng giác thường gặp

I. TÓM TẮT LÝ THUYẾT

1. Phương trình bậc nhất với một hàm số lượng giác:

- Định nghĩa: Phương trình bậc nhất đối với một hàm số lượng giác là phương trình có dạng: at + b = 0, trong đó a, b là các hằng số (a ≠ 0) và t là một trong các hàm số lượng giác.

- Ví dụ: 2sin x + 1 = 0 là phương trình bậc nhất đối với sin x,…

2. Phương trình bậc hai đối với một hàm số lượng giác

- Định nghĩa: Phương trình bậc hai đối với một hàm số lượng giác là phương trình có dạng: at² + bt + c = 0, trong đó a, b, c là các hằng số (a ≠ 0) và t là một trong các hàm số lượng giác.

- Ví dụ: 3tan² x 2tan x 1 = 0 là phương trình bậc hai đối với tan x

3. Phương trình bậc nhất đối với sin x và cos x

- Công thức biến đổi biểu thức asin x + bcos x :

    asin x + bcos x = 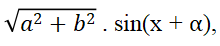        (1)

    với 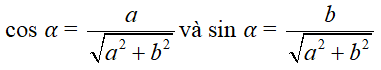(a² + b² ≠ 0)

- Xét phương trình: asin x + bcos x = c        (2)

với a, b, c ∈ R; a, b không đồng thời bằng 0 (a² + b² ≠ 0).

+ Nếu a = 0, b ≠ 0 hoặc a ≠ 0, b = 0, phương trình (2) có thể đưa ngay về phương trình lượng giác cơ bản.

+ Nếu a ≠ 0, b ≠ 0, ta áp dụng công thức (1)

II. PHƯƠNG PHÁP GIẢI

1. Phương trình bậc nhất với một hàm số lượng giác:

- Cách giải:

+ Bước 1: Chuyển vế

+ Bước 2: Chia hai vế của phương trình đã cho cho a

+ Bước 3: Giải phương trình lượng cơ bản.

- Ví dụ: Giải phương trình: 2sin x – √3 = 0

Ta có: 2sin x – √3 = 0 ⇔ 2sin x = √3

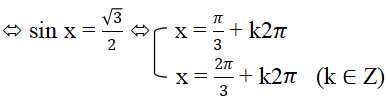
2. Phương trình bậc hai đối với một hàm số lượng giác:

- Cách giải:

+ Bước 1: Đặt biểu thức lượng giác làm ẩn phụ và đặt điều kiện cho ẩn phụ (nếu có)

+ Bước 2: Giải phương trình bậc hai theo ẩn phụ này

+ Bước 3: Ta đưa về việc giải các phương trình lượng giác cơ bản.

- Ví dụ: Giải phương trình:

    3cos²x – 2cos x – 1 = 0

Đặt cos x = t với điều kiện –1 ≤ t ≤ 1 (*)

Khi đó phương trình đã cho có dạng: 3t² – 2t – 1 = 0 (**)

Giải phương trình (**) ta được hai nghiệm t₁ = 1 và t₂ = -1/3 thoả mãn điều kiện (*)

Vậy ta có:

TH1: cos x = 1 ⇔ x = k2π    (k ∈ Z).

TH2: cos x = -1/3 ⇔ x = ±arccos (-1/3) + k2π    (k ∈ Z)