Các dạng bài tập Xác suất chọn lọc, có lời giải - Toán lớp 11

---

Các dạng bài tập Xác suất chọn lọc, có lời giải

Với Các dạng bài tập Xác suất chọn lọc, có lời giải Toán lớp 11 tổng hợp các dạng bài tập, 100 bài tập trắc nghiệm có lời giải chi tiết với đầy đủ phương pháp giải, ví dụ minh họa sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Xác suất từ đó đạt điểm cao trong bài thi môn Toán lớp 11.

• Dạng 1: Xác định phép thử, không gian mẫu và biến cố Xem chi tiết
• Trắc nghiệm xác định phép thử, không gian mẫu và biến cố Xem chi tiết
• Dạng 2: Tính xác suất theo định nghĩa cổ điển Xem chi tiết
• Trắc nghiệm tính xác suất theo định nghĩa cổ điển Xem chi tiết
• Dạng 3: Các quy tắc tính xác suất Xem chi tiết
• Trắc nghiệm các quy tắc tính xác suất Xem chi tiết
• Cách xác định phép thử, không gian mẫu cực hay có lời giải Xem chi tiết
• Cách tìm xác suất của biến cố cực hay có lời giải Xem chi tiết
• Cách tính xác suất bài toán liên quan đến đếm số cực hay có lời giải Xem chi tiết
• Cách tính xác suất bài toán liên quan đến hình học cực hay có lời giải Xem chi tiết
• Cách giải bài tập Xác suất nâng cao, cực hay có lời giải Xem chi tiết
• Phương pháp giải bài tập về Quy tắc cộng xác suất cực hay có lời giải Xem chi tiết
• Phương pháp giải bài tập về Biến cố đối cực hay có lời giải Xem chi tiết
• Phương pháp giải bài tập về Quy tắc nhân xác suất cực hay có lời giải Xem chi tiết
• 60 bài tập trắc nghiệm Xác suất chọn lọc, có lời giải Xem chi tiết

Cách xác định phép thử, không gian mẫu và biến cố

A. Phương pháp giải & Ví dụ

Để xác định không gian mẫu và biến cố ta thường sử dụng các cách sau

Cách 1: Liệt kê các phần tử của không gian mẫu và biến cố rồi chúng ta đếm.

Cách 2: Sử dụng các quy tắc đếm để xác định số phần tử của không gian mẫu và biến cố.

Ví dụ minh họa

Bài 1: Trong một chiếc hộp đựng 6 viên bi đỏ, 8 viên bi xanh, 10 viên bi trắng. Lấy ngẫu nhiên 4 viên bi. Tính số phần tử của:

1. Không gian mẫu

2. Các biến cố:

A: " 4 viên bi lấy ra có đúng hai viên bi màu trắng"

B: " 4 viên bi lấy ra có ít nhất một viên bi màu đỏ"

C: " 4 viên bi lấy ra có đủ 3 màu"

Đáp án và hướng dẫn giải

1.

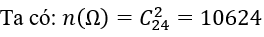
2. Số cách chọn 4 viên bi có đúng hai viên bị màu trắng là:

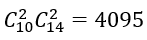
Suy ra: n(Ω)=4095

Số cách lấy 4 viên bi mà không có viên bi màu đỏ được chọn là:

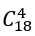
Suy ra :

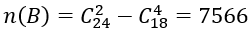
Số cách lấy 4 viên bi chỉ có một màu là:

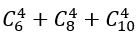
Số cách lấy 4 viên bi có đúng hai màu là:

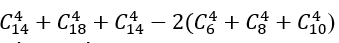
Số cách lấy 4 viên bị có đủ ba màu là:

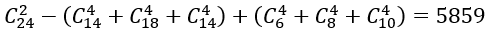
Suy ra n(C)=5859

Bài 2: Một xạ thủ bắn liên tục 4 phát đạn vào bia. Gọi A_k là các biến cố " xạ thủ bắn trúng lần thứ k" với k = 1,2,3,4. Hãy biểu diễn các biến cố sau qua các biến cố A₁, A₂, A₃, A₄

A: "Lần thứ tư mới bắn trúng bia’’

B: "Bắn trúng bia ít nhất một lần’’

C: " Chỉ bắn trúng bia hai lần’’

Đáp án và hướng dẫn giải

Ta có: Giả sử 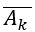là biến cố lần thứ k (k = 1,2,3,4) bắn không trúng bia.

Do đó:

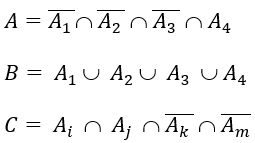
với i,k,k,m ∈ {1,2,3,4} và đôi một khác nhau.

Cách tính xác suất theo định nghĩa cổ điển

A. Phương pháp giải & Ví dụ

♦ Tính xác suất theo thống kê ta sử dụng công thức:

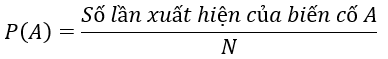
♦ Tính xác suất của biến cố theo định nghĩa cổ điển ta sử dụng công thức :

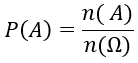
Ví dụ minh họa

Bài 1: Bộ bài tú - lơ khơ có 52 quân bài. Rút ngẫu nhiên ra 4 quân bài. Tìm xác suất của các biến cố:

A: "Rút ra được tứ quý K ‘’

B: "4 quân bài rút ra có ít nhất một con Át"

C: "4 quân bài lấy ra có ít nhất hai quân bích’’

Đáp án và hướng dẫn giải

Ta có số cách chọn ngẫu nhiên 4 quân bài là:

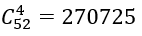
Suy ra n(Ω ) = 270725

Vì bộ bài chỉ có 1 tứ quý K nên ta có n(A)=1

Vậy P(A) = 1 /270725

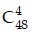
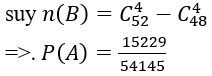
Vì có cách rút 4 quân bài mà không có con Át nào

Vì trong bộ bài có 13 quân bích, số cách rút ra bốn quân bài mà trong đó số quân bích không ít hơn 2 là:

Bài 2: Trong một chiếc hộp có 20 viên bi, trong đó có 8 viên bi màu đỏ, 7 viên bi màu xanh và 5 viên bi màu vàng. Lấy ngẫu nhiên ra 3 viên bi. Tìm xác suất để:

1. 3 viên bi lấy ra đều màu đỏ

2. 3 viên bi lấy ra có không quá hai màu.

Đáp án và hướng dẫn giải

Gọi biến cố A :" 3 viên bi lấy ra đều màu đỏ"

B : "3 viên bi lấy ra có không quá hai màu"

Số các lấy 3 viên bi từ 20 viên bi là:

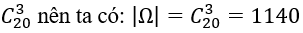
1. Số cách lấy 3 viên bi màu đỏ là:

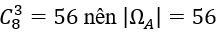
Do đó:

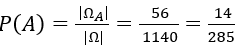
2. Ta có:

Số cách lấy 3 viên bi chỉ có một màu:

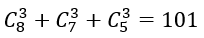
Số các lấy 3 viên bi có đúng hai màu

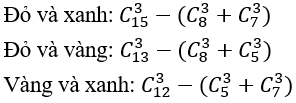
Nên số cách lấy 3 viên bi có đúng hai màu:

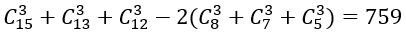
Do đó: |Ω_B | = 860. Vậy:

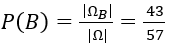
Cách tìm xác suất của biến cố

A. Phương pháp giải

Cho phép thử T có không gian mẫu Ω và A là một biến cố liên quan với phép thử T.

Để tính được xác suất của biến cố A ta cần xác định:

+ Số phần tử của không gian mẫu.

+ Số kết quả thuận lợi cho biến cố A

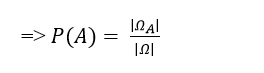
B. Ví dụ minh họa

Ví dụ 1: Gieo một đồng tiền liên tiếp 3 lần.Tính xác suất của biến cố A: “kết quả của 3 lần gieo là như nhau”

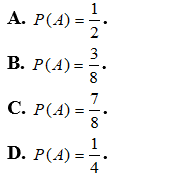
Hướng dẫn giải :

Đáp án : D

Số phần tử của không gian mẫu là:

Lần đầu có thể ra tùy ý nên có 2 khả năng xảy ra.

Lần 2 và 3 phải giống lần 1 nên lần 2 và 3 chỉ có 1 khả năng.

Khi đó n(A)=2.1.1=2

Xác suất của biến cố A là n(A)=2/8=1/4

Ví dụ 2: Gieo đồng tiền 5 lần cân đối và đồng chất. Xác suất để được ít nhất một lần xuất hiện mặt sấp là:

A.31/32    B.21/32    C.11/32    D.1/32

Hướng dẫn giải :

Đáp án : A

Phép thử : Gieo đồng tiền 5 lần cân đối và đồng chất.

Ta có n(Ω)=2⁵=32.

Biến cố A : Được ít nhất một lần xuất hiện mặt sấp.

Biến cố đối A tất cả đều là mặt ngửa

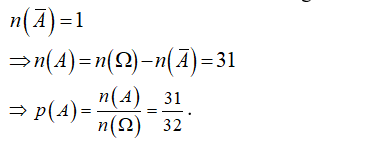
Ví dụ 3: Gieo một đồng tiền liên tiếp 3 lần. Tính xác suất của biến cố A: “có đúng 2 lần xuất hiện mặt sấp”.

A.P(A)=1/2    B.P(A)=3/8    C.P(A)=7/8    D.P(A)=1/4

Hướng dẫn giải :

Đáp án : B

Số phần tử của không gian mẫu là: 2³=8

Các kết quả thuận lợi cho biến cố A là:

Ω_A = { SSN; SNS: NSS}

⇒ n(A)= 3

Do đó; xác suất của biến cố A là: P(A)= 3/8