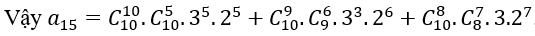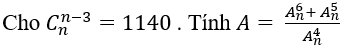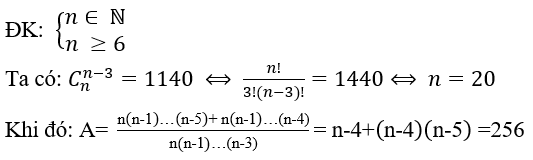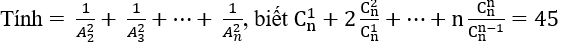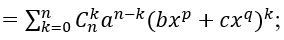Các dạng bài tập Tổ hợp chọn lọc, có lời giải - Toán lớp 11
Các dạng bài tập Tổ hợp chọn lọc, có lời giải
Với Các dạng bài tập Tổ hợp chọn lọc, có lời giải Toán lớp 11 tổng hợp các dạng bài tập, 100 bài tập trắc nghiệm có lời giải chi tiết với đầy đủ phương pháp giải, ví dụ minh họa sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Tổ hợp từ đó đạt điểm cao trong bài thi môn Toán lớp 11.

- Bài toán đếm số phương án Xem chi tiết
- Cách giải bài toán đếm số phương án Xem chi tiết
- Dạng 1:Đếm số phương án liên quan đến số tự nhiên Xem chi tiết
- Trắc nghiệm đếm số phương án liên quan đến số tự nhiên Xem chi tiết
- Dạng 2:Đếm số phương án liên quan đến kiến thức thực tế Xem chi tiết
- Trắc nghiệm đếm số phương án liên quan đến kiến thức thực tế Xem chi tiết
- Dạng 3: Bài toán đếm số tự nhiên Xem chi tiết
- Trắc nghiệm bài toán đếm số tự nhiên Xem chi tiết
- Dạng 4: Bài toán xếp vị trí, phân công công việc Xem chi tiết
- Trắc nghiệm bài toán xếp vị trí, phân công công việc Xem chi tiết
- Dạng 5: Bài toán tổ hợp trong hình học Xem chi tiết
- Trắc nghiệm bài toán tổ hợp trong hình học Xem chi tiết
- Dạng 6: Giải phương trình, bất phương trình tổ hợp Xem chi tiết
- Trắc nghiệm giải phương trình, bất phương trình tổ hợp Xem chi tiết
- Dạng 7: Xác định hệ số, số hạng trong khai triển nhị thức Niu-tơn Xem chi tiết
- Trắc nghiệm xác định hệ số, số hạng trong khai triển nhị thức Niu-tơn Xem chi tiết
- Dạng 8: Tính tổng trong nhị thức Niu-tơn Xem chi tiết
- Trắc nghiệm tính tổng trong nhị thức Niu-tơn Xem chi tiết
- Phương pháp giải bài tập về quy tắc cộng cực hay có lời giải Xem chi tiết
- Bài tập về quy tắc cộng nâng cao cực hay có lời giải Xem chi tiết
- Phương pháp giải bài tập về quy tắc nhân cực hay có lời giải Xem chi tiết
- Phương pháp giải bài toán đếm số cực hay có lời giải Xem chi tiết
- Phương pháp giải bài toán đếm hình cực hay có lời giải Xem chi tiết
- Phương pháp giải bài tập Hoán vị cực hay có lời giải Xem chi tiết
- Cách giải bài toán đếm số sử dụng Hoán vị cực hay có lời giải Xem chi tiết
- Phương pháp giải bài toán Hoán vị vòng quanh cực hay có lời giải Xem chi tiết
- Phương pháp giải bài toán Hoán vị lặp cực hay có lời giải Xem chi tiết
- Phương pháp giải bài tập Chỉnh hợp cực hay có lời giải Xem chi tiết
- Cách giải bài toán đếm số sử dụng Chỉnh hợp cực hay có lời giải Xem chi tiết
- Phương pháp giải bài tập Tổ hợp cực hay có lời giải Xem chi tiết
- Cách giải bài toán đếm số sử dụng Tổ hợp cực hay có lời giải Xem chi tiết
- Cách giải bài toán đếm hình sử dụng Tổ hợp cực hay có lời giải Xem chi tiết
- Cách khai triển nhị thức Newton: tìm hệ số, số hạng trong khai triển cực hay Xem chi tiết
- Tìm số hạng chứa x^a trong khai triển đa thức P cực hay có lời giải Xem chi tiết
- Cách tìm hệ số lớn nhất trong khai triển cực hay có lời giải Xem chi tiết
- Bài tập về nhị thức Newton nâng cao cực hay có lời giải Xem chi tiết
- 60 bài tập trắc nghiệm Tổ hợp chọn lọc, có lời giải Xem chi tiết
Cách giải bài toán đếm số tự nhiên
A. Phương pháp giải & Ví dụ
Dựa vào hai quy tắc cộng, quy tắc nhân và các khái niệm hoán vị, chỉnh hợp, tổ hợp, đếm gián tiếp, đếm phần bù.
Một số dấu hiệu giúp chúng ta nhận biết được hoán vị, chỉnh hợp hay tổ hợp.
1) Hoán vị: Các dấu hiệu đặc trưng để giúp ta nhận dạng một hoán vị của n phần tử là:
♦ Tất cả n phần tử đều phải có mặt
♦ Mỗi phần tử xuất hiện một lần.
♦ Có thứ tự giữa các phần tử.
2) Chỉnh hợp: Ta sẽ sử dụng khái niệm chỉnh hợp khi:
♦ Cần chọn k phần tử từ n phần tử, mỗi phần tử xuất hiện một lần
♦ k phần tử đã cho được sắp xếp thứ tự.
3) Tổ hợp: Ta sử dụng khái niệm tổ hợp khi:
♦ Cần chọn k phần tử từ n phần tử, mỗi phần tử xuất hiện một lần
♦ Không quan tâm đến thứ tự k phần tử đã chọn.
Ví dụ minh họa
Bài 1: Từ các số 0,1,2,3,4,5 có thể lập được bao nhiêu số tự mà mỗi số có 6 chữ số khác nhau và chữ số 2 đứng cạnh chữ số 3?
Đặt y = 23, xét các số 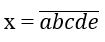
trong đó a,b,c,d,e đôi một khác nhau và thuộc tập {0,1,y,4,5}.
Số cách chọn một số thỏa mãn điều kiện trên là một hoán vị của 5 phần tử (tính cả trường hợp a = 0). Vậy có P5 số.
Nếu a = 0 thì số số lập được với a,b,c,d,e như trên là P4.
Vậy có (P5 - P4) = 96 số có 5 chữ số thỏa mãn điều kiện trên.
Khi ta hoán vị 2,3 trong y ta được hai số khác nhau
Nên có 96.2 = 192 số thỏa yêu cầu bài toán.
Cách giải phương trình, bất phương trình tổ hợp
A. Phương pháp giải & Ví dụ
Dựa vào công thức tổ hợp, chỉnh hợp hoán vị để chuyển phương trình, bất phương trình, hệ phương trình tổ hợp về phương trình, bất phương trình, hệ phương trình đại số.
Ví dụ minh họa
Bài 1:
Đáp án và hướng dẫn giải
Bài 2:
Đáp án và hướng dẫn giải
Xác định hệ số, số hạng trong khai triển nhị thức Niu-tơn
Xác định hệ số, số hạng trong khai triển nhị thức Niu-tơn
A. Phương pháp giải & Ví dụ
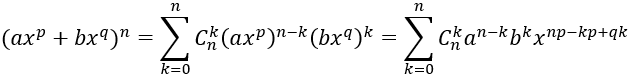
Số hạng chứa xm ứng với giá trị k thỏa mãn: np – pk + qk = m.
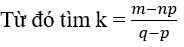
Vậy hệ số của số hạng chứa xm là: 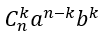
Nếu k không nguyên hoặc k > n thì trong khai triển không chứa xm , hệ số phải tìm bằng 0.
Chú ý: Xác định hệ số của số hạng chứa xm trong khai triển P(x) = (a + bxp + cxq)n
P(x) = (a + bxp + cxq)n được viết dưới dạng a0 + a1x + ...+ a2nx2n
Ta làm như sau:
* Viết P(x) = (a + bxp + cxq)n
* Viết số hạng tổng quát khi khai triển các số hạng dạng (bxp+cxq)k thành một đa thức theo luỹ thừa của x.
* Từ số hạng tổng quát của hai khai triển trên ta tính được hệ số của xm.
Chú ý: Để xác định hệ số lớn nhất trong khai triển nhị thức Niutơn
Ta làm như sau:
* Tính hệ số ak theo k và n;
* Giải bất phương trình ak-1 ≤ ak với ẩn số k;
* Hệ số lớn nhất phải tìm ứng với số tự nhiên k lớn nhất thoả mãn bất phương trình trên.
Ví dụ minh họa
Bài 1: Tìm hệ số của x5 trong khai triển đa thức của: x(1-2x)5+x2 (1+3x)10
Đáp án và hướng dẫn giải
Đặt f(x)=x(1-2x)5+x2 (1+3x)10
Ta có :
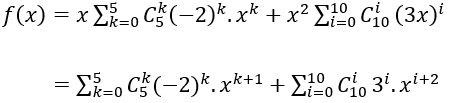
Vậy hệ số của x5 trong khai triển đa thức của f(x) ứng với k = 4 và i = 3 là:
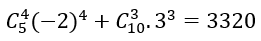
Bài 2: Đa thức P(x) =(1+3x+2x2)10=a0 + a1 x + ⋯ + a20 x20. Tìm a15
Đáp án và hướng dẫn giải
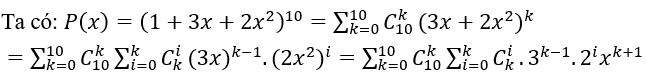
với 0 ≤ i ≤ k ≤ 10. Do đó k + i = 15 với các trường hợp
k=10, i=5 hoặc k=9, i=6 hoặc k=8, i=7