Bài 11 trang 33 Chuyên đề Toán 11 Cánh diều
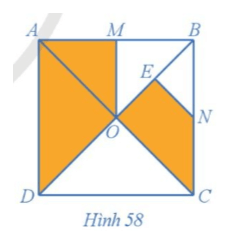
Cho hình vuông ABCD có hai đường chéo cắt nhau tại O. Gọi M, N, E lần lượt là trung điểm của AB, BC, BO (). Chứng minh rằng hai hình AMOD và OENC đồng dạng với nhau.
Giải Chuyên đề Toán 11 Bài 2: Phép đồng dạng - Cánh diều
Bài 11 trang 33 Chuyên đề Toán 11: Cho hình vuông ABCD có hai đường chéo cắt nhau tại O. Gọi M, N, E lần lượt là trung điểm của AB, BC, BO (Hình 58). Chứng minh rằng hai hình AMOD và OENC đồng dạng với nhau.
Lời giải:
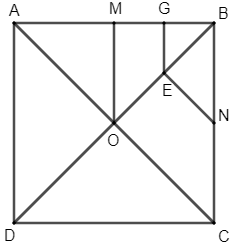
Gọi G là trung điểm của BM.
Khi đó, ta thấy Hình 58 và Hình 56 là hai hình giống nhau.
+) Theo kết quả Ví dụ 8 trang 32 thì hai hình BGEN và AMOD đồng dạng với nhau (1).
+) Theo kết quả Luyện tập 4 trang 32 thì hai hình OMGE và COEN đồng dạng với nhau hay hai hình MGEO và OENC đồng dạng với nhau (2).
+) Thực hiện phép đối xứng trục GE thì hình BGEN biến thành hình MGEO (3).
Do đó, hai hình BGEN và MGEO đồng dạng với nhau.
Từ (1), (2) và (3) suy ra hai hình AMOD và OENC đồng dạng với nhau.
Lời giải Chuyên đề Toán 11 Bài 2: Phép đồng dạng hay, chi tiết khác:
Bài 3 trang 32 Chuyên đề Toán 11: Khẳng định nào dưới đây là đúng? ....
Bài 5 trang 33 Chuyên đề Toán 11: Một thấu kính phân kì có tiêu cự OF = OF' = 20 cm (kính cận). ....