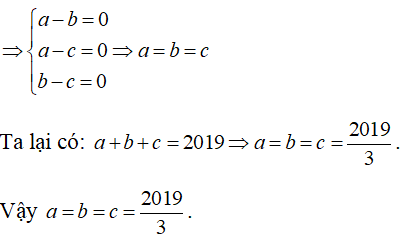Đề thi Toán lớp 8 Giữa kì 1 năm 2024 có đáp án (4 đề)

---

Đề thi Toán lớp 8 Giữa kì 1 năm 2024 có đáp án (4 đề)

Haylamdo biên soạn và sưu tầm Đề thi Toán lớp 8 Giữa kì 1 năm 2024 có đáp án (4 đề) được tổng hợp chọn lọc từ đề thi môn Toán 8 của các trường trên cả nước sẽ giúp học sinh có kế hoạch ôn luyện từ đó đạt điểm cao trong các bài thi Toán lớp 8.

Phòng Giáo dục và Đào tạo .....

Đề khảo sát chất lượng Giữa kì 1

Năm học 2024

Môn: Toán 8

Thời gian làm bài: 90 phút

(Đề thi số 1)

Câu 1 (2 điểm) Phân tích đa thức thành nhân tử

a. 8x² - 8xy - 4x + 4y       b. x³ + 10x² + 25x - xy²

c. x² + x - 6       d. 2x² + 4x - 16

Câu 2 (2 điểm) Tìm giá trị của x, biết:

a. x³ - 16x = 0       b. (2x + 1)² - (x - 1)² = 0

Câu 3 (2 điểm) Chứng minh biểu thức sau không phụ thuộc vào x

a. A = (2x - 1)(4x² + 2x + 1) - (2x + 1)(4x² - 2x + 1)

b. B = x(2x + 1) - x²(x + 2) + x³ - x + 5

Câu 4 (1 điểm) Tính giá trị nhỏ nhất của biểu thức P = x² - 2xy + 6y² - 12x + 2y + 45

Câu 5 (2 điểm) Cho hình thang ABDC (AB // CD). Trên cạnh AD lấy điểm M và N sao cho AM = MN = NC. Từ M và N kẻ các đường thẳng song song với hai đáy cắt BC theo thứ tự E và F. Chứng minh rằng:

a. BE = EF = FD

b. Cho CD = 8cm, ME = 6cm. Tính độ dài AB và FN

Câu 6 (0.5 điểm) Cho x, y, z là các số dương. Tìm giá trị nhỏ nhất của:

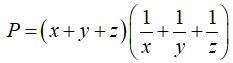
Đáp án và Hướng dẫn làm bài

Câu 1:

a. 8x² - 8xy - 4x + 4y = 8x(x - y) - 4(x - y) = (x - y)(8x - 4) = 4(x - y)(2x - 1)

b.

x³ + 10x² + 25x - xy² = x(x² + 10x + 25 - y²) = x[(x - 5)² - y²] = x(x - 5 - y)(x - 5 + y)

c. x² + x - 6 = x² - 2x + 3x - 6 = x(x - 2) + 3(x - 2) = (x - 2)(x + 3)

d.

2x² + 4x - 16 = 2(x² - 2x - 8) = 2(x² - 2x + 1 - 9)

= 2[(x - 1)² - 9] = 2(x - 1 - 9)(x - 1 + 9) = 2(x - 10)(x + 8)

Câu 2:

a.

x³ - 16x = 0

x(x² - 16) = 0

x(x - 4)(x + 4) = 0

Suy ra x = 0, x = 4, x = -4

b.

(2x + 1)² - (x - 1)² = 0

(2x + 1 - x + 1)(2x + 1 + x - 1) = 0

(x + 2)(3x) = 0

Suy ra x = 0 hoặc x = -2

Câu 3:

a.

A = (2x - 1)(4x² + 2x + 1) - (2x + 1)(4x² - 2x + 1)

A = (2x)³ - 1 - [(2x)³ + 1]

A = 8x³ - 1 - 8x³ - 1

A = -2

Vậy giá trị của biểu thức A không phụ thuôc vào giá trị của x.

b.

B = x(2x + 1) - x²(x + 2) + x³ - x + 5

B = 2x² + x - x³ - 2x² + x³ - x + 5

B = 5

Vậy biểu thức không phụ thuộc vào x

Câu 4:

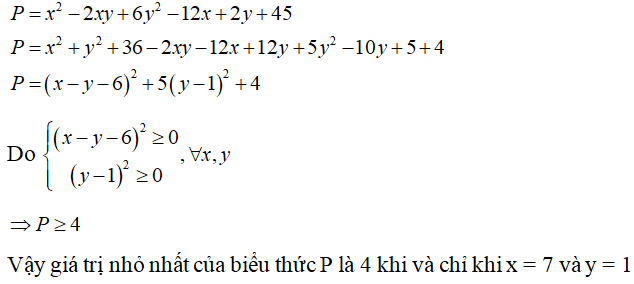
Câu 5:

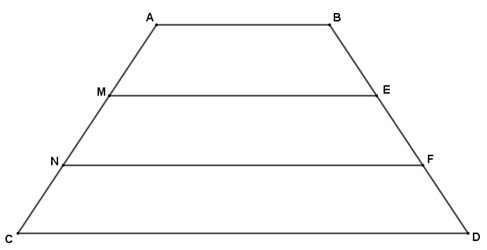
a. Ta có ABCD là hình thang AB // CD

Ta có AB // CD, FN // CD suy ra AB // NF

Vậy ABFN là hình thang (dấu hiệu nhận biết).

Xét hình thang ABFN có ME // NF, ME = NF nên ME là đường trung bình của hình thang ABFN

Suy ra BE = EF.

Xét tương tự với hình thang MEDC ta suy ra EF = FD

Ta có điều phải chứng minh.

b. Theo chứng minh trên ta có

Câu 6:

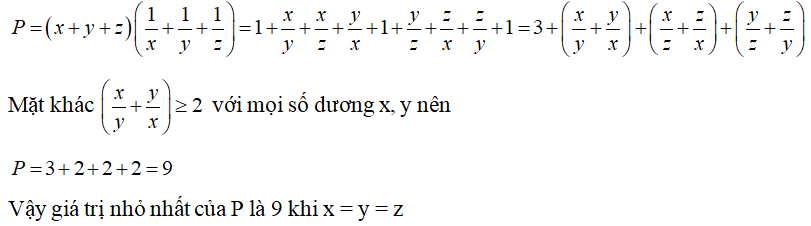
Phòng Giáo dục và Đào tạo .....

Đề khảo sát chất lượng Giữa kì 1

Năm học 2024

Môn: Toán 8

Thời gian làm bài: 90 phút

(Đề thi số 2)

PHẦN I: TRẮC NGHIỆM (2 điểm)

Hãy viết chữ cái in hoa đứng trước phương án đúng trong mỗi câu sau vào bài làm.

Câu 1: Kết quả phép tính x(x - y) + y(x + y) tại x = -3 và y = 4 là:

A. 1       B. 7       C. -25

Câu 2: Khai triển biểu thức (x - 2y)³ ta được kết quả là:

A. x³ - 8y³       B. x³ - 2y³

C. x³ - 6x²y + 6xy² - 2y³       D. x³ - 6x²y + 12xy² - 8y³

Câu 3: Giá trị biểu thức 2009² - 2018.2009 + 1009² có bao nhiêu chữ số 0 ?

A. 6       B. 2       C. 4

Câu 4: Đa thức 4x² - 12x + 9 phân tích thành nhân tử là:

A. (2x - 3)²       B. 2x + 3       C. 4x - 9

Câu 5: Hình nào sau đây là tứ giác có hai đường chéo bằng nhau?

A. Hình thang       B. Hình thang cân

C. Hình thang vuông       D. Hình bình hành

Câu 6: Cho tam giác ABC có cạnh BC = 8cm và D, E, M, N lần lượt là trung điểm của AB, AC, BD và CE (như hình vẽ). Khi đó, độ dài của MN là

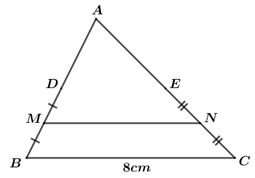
A. 7cm       B. 5cm       C. 6cm       D. 4cm

Câu 7: Cho hình bình hành ABCD có ∠A = 60^o. Khi đó, hệ thức nào sau đây là không đúng?

Câu 8: Hình chữ nhật có độ dài cạnh 5cm và 12cm thì khoảng cách từ giao điểm hai đường chéo đến mỗi đỉnh là

A. 17cm       B. 8,5cm       C. 6,5cm       D. 13cm

PHẦN II: TỰ LUẬN (8 điểm)

Câu 1 (VD) (2,25 điểm)

Rút gọn các biểu thức sau:

a. 2x(3x + 2) - 3x(2x + 3)

b. (x + 2)³ + (x - 3)² - x²(x + 5)

c. (3x³ - 4x² + 6x) : 3x

Câu 2 (VD) (0,75 điểm)

Phân tích đa thức sau thành nhân tử: 2x³ - 12x² + 18x

Câu 3 (VD) (1,0 điểm)

Tìm x, biết: 3x(x - 5) - x² + 25 = 0

Câu 4 (VD) (3,0 điểm) Cho hình bình hành ABCD (AB > AD). Gọi E và K lần lượt là trung điểm của CD và AB. BD cắt AE, AC, CK lần lượt tại N, O và I. Chứng minh rằng:

a. Tứ giắc AECK là hình bình hành.

b. Ba điểm E, O, K thẳng hàng.

c. DN = NI = IB

d. AE = 3KI

Câu 5 (VDC) (1,0 điểm) Cho x, y là hai số thực tùy ý, tìm giá trị nhỏ nhất của biểu thức sau:

P = x² + 5y² + 4xy + 6x + 16y + 32

Đáp án và Hướng dẫn làm bài

A. PHẦN TRẮC NGHIỆM

Câu 1:

Thay x = -3 và y = -4 vào biểu thức x(x - y) + y(x + y) ta được:

(-3)(-3 - 4) + 4(-3 + 4) = 21 + 4 = 25

Chọn D.

Câu 2:

Ta có:

(x - 2y³ = x³ - 3x².2y + 3x.(2y)² + (2y)³ = x³ - 6x²y + 12xy² - 8y³

Chọn D.

Câu 3:

2009² - 2018.2009 + 1009²

2009² - 2.2009.1009 + 1009²

= (2009 - 1009)²

= 1000²

= 1000000

Vậy giá trị của biểu thức 2009² - 2018.2009 + 1009² có 6 chữ số 0.

Chọn A.

Câu 4:

4x² - 12x + 9 = (2x)² - 2.2x.3 + 3² = (2x - 3)²

Chọn A.

Câu 5:

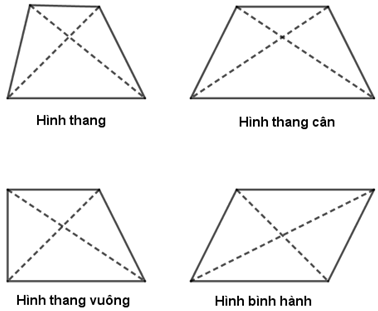
Quan sát hình vẽ, và áp dụng tính chất của các hình ta có: Hình thang cân là hình có hai đường chéo bằng nhau.

Chọn B.

Câu 6:

Chọn D.

Câu 7:

Vì ABCD là hình bình hành nên ta có: ∠A = ∠C, ∠B = ∠D và AB // CD, AD // BC

Mà ∠A = 60^o ⇒ ∠C = 60^o

⇒ Đáp án C đúng.

Vì AD // BC mà ∠A và ∠B ở vị trí trong cùng phía nên ta có: ∠A + ∠B = 180^o ⇒ ∠B = 120^o

⇒ ∠B = 2∠C ⇒ Đáp án B đúng.

⇒ ∠A = ∠B/2 ⇒ Đáp án D đúng.

Vì AB // CD mà ∠A và ∠D ở vị trí trong cùng phía nên ta có: ∠A + ∠D = 180^o ⇒ ∠D = 120^o

⇒ Đáp án A sai.

Chọn A.

Câu 8:

Chọn C.

PHẦN II: TỰ LUẬN

Bài 1.

a.

2x(3x + 2) - 3x(2x + 3)

= 2x.3x + 2x.2 - 3x.2x - 3x.3

= 6x² + 4x - 6x² - 9x

= -5x

b.

(x + 2)³ + (x - 3)³ - x²(x + 5)

= (x³ + 6x² + 12x + 8) + (x² - 6x + 9) - (x³ + 5x²)

= x³ + 6x² + 12x + 8 + x² - 6x + 9 - x³ - 5x²

= (x³ - x³) + (6x² + x² - 5x²) + (12x - 6x) + 9

= 2x² + 6x + 9

c.

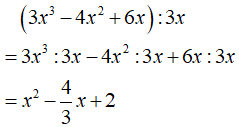
Bài 2.

2x³ - 12x² + 18x

= 2x(x² - 6x + 9)

= 2x(x - 3)²

Bài 3.

3x(x - 5) - x² + 25 = 0

3x(x - 5) - (x² + 25) = 0

3x(x - 5) - (x + 5)(x - 5) = 0

(3x - x - 5)(x - 5) = 0

(2x - 5)(x - 5) = 0

Bài 4.

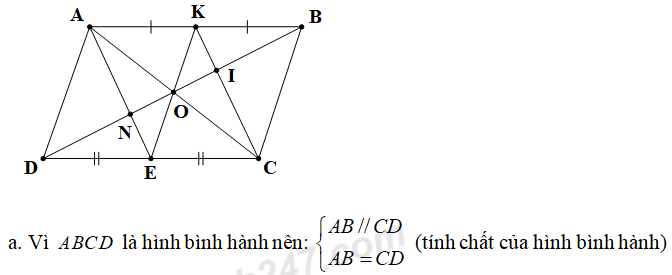
Mà E, K lần lượt là trung điểm của CD và AB nên AK = EC VÀ AK // EC.

⇒ Tứ giác AECK là hình bình hành (dấu hiệu nhận biết)

b. Trong hình bình hành ABCD có O là giao điểm của hai đường chéo nên O là trung điểm của AC và BD (tính chất của hình bình hành)

Mà AECK là hình bình hành nên O là trung điểm của EK.

⇒ Ba điểm E, O, K thẳng hàng.

Bài 5.

P = x² + 5y² + 4xy + 6x + 16y + 32

⇒ P = x² + (4xy + 6x) + 5y² + 16y + 32

⇒ P = x² + 2x(2y + 3) + (2y + 3)² - (2y + 3)² + 5y² + 16y + 32

⇒ P = [x + (2y + 3)]² - 4y² - 12y - 9 + 5y² + 16y + 32

⇒ P = (x + 2y + 3)² + y² + 4y + 23

⇒ P = (x + 2y + 3)² + (y + 2)² + 19

Vì (x + 2y + 3)² ≥ 0 với mọi x, y ∈ R

(y + 2)² ≥ 0 với mọi y ∈ R

⇒ P = (x + 2y + 3)² + (y + 2)² + 19 ≥ 19 với mọi x, y ∈ R

Dấu "=" xảy ra khi và chỉ khi x + 2y + 3 = 0 và y + 2 =0

Suy ra, x = 1 và y = -2

Vậy P đạt giá trị nhỏ nhất bằng 19 tại x = 1 và y = -2.

Phòng Giáo dục và Đào tạo .....

Đề khảo sát chất lượng Giữa kì 1

Năm học 2024

Môn: Toán 8

Thời gian làm bài: 90 phút

(Đề thi số 3)

Câu 1: Phân tích đa thức thành nhân tử:

a. 2x² - 3x - 2       b. 4x(x - 2) + 3(2 - x)

c. 27x³ + 8       d. x² + 2x - y² + 1

Câu 2 (2 điểm): Tìm giá trị của x, biết:

a. 9x² + 6x - 3 = 0       b. x(x - 2)(x + 2) - (x + 2)(x² - 2x + 4) = 4

Câu 3 (2 điểm): Rút gọn và tính giá trị biểu thức:

a. A = x(x + y) - 5(x + y) với x = 1, y = 2

b. B = 3x(x² - 3) + x²(4 - 3x) - 4x² + 1 tại x = 1/9

Câu 4:

Cho hình thang vuông ABCD (∠A = ∠D = 90^o) và CD = 2AB. Kẻ DH vuông góc với AC (H ∈ AC). Gọi M là trung điểm của HC, N là trung điểm của DH. Chứng minh rằng:

a. MN ⊥ AD

b. ABMN là hình bình hành.

c. ∠BMD = 90^o

Câu 5:

1) Cho biểu thức: A = (2x - 3)² - (x + 1)(x + 5) + 2

Rút gọn và tìm giá trị nhỏ nhất của A.

2) Cho B = n² - 27n² + 121. Tìm số tự nhiên n để B là số nguyên.

Đáp án và Hướng dẫn làm bài

Câu 1:

a.

2x² - 3x - 2 = 2x² - 4x + x - 2 = (2x² - 4x) + (x - 2)

= 2x(x - 2) + (x - 2) = (x - 2)(2x + 1)

b.

4x(x - 2) + 3(2 - x) = 4x(x - 2) - (x - 2) = (x - 2)(4x - 1)

c.

27x³ + 8 = (3x)³ + 2³ = (3x + 2)[(3x)² - 2.3x + 2²] = (3x + 2)(9x² - 6x + 2)

d.

x² + 2x - y² + 1 = (x² + 2x + 1) - y² = (x + 1)² - y²

= (x + 1 - y)(x + 1 + y)

Câu 2:

a.

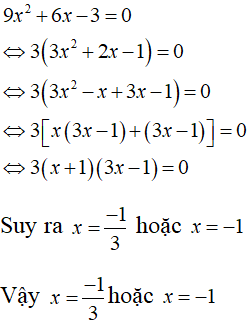
b.

x(x - 2)(x + 2) - (x + 2)(x² - 2x + 4) = 4

⇔ x(x² - 4) - (x³ + 8) = 4

⇔ x³ - 4x - x³ - 8 - 4 = 0

⇔ -4x = 12

⇔ x = -3

Suy ra x = -3

Vậy x = -3

Câu 3:

a.

A = x(x + y) - 5(x + y) = (x + y)(x - 5) (*)

Thay x = 1, y = 2 vào biểu thức (*) ta có:

A = (1 + 2)(1 - 5) = 3.(-4) = -12

Vậy với x = 1, y = 2 thì A = -12

b. (1 điểm)

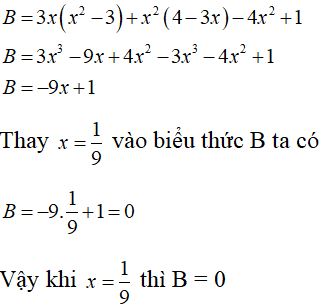
Câu 4:

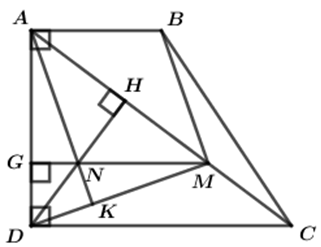
a. Vì ABCD là hình thang vuông nên ∠A = ∠D = 90^o

⇒ AD ⊥ DC tại D (1)

Xét tam giác HDC ta có:

NH = ND (giả thiết)

MH = Mc (giả thiết)

⇒ NM là đường trung bình của tam giác HDC

⇒ NM // DC (2)

Từ (1) và (2) suy ra MN ⊥ AD tại G (từ vuông góc đến song song)

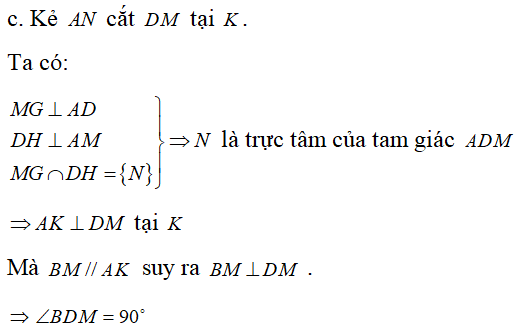
Câu 5:

1) A = (2x - 3)² - (x + 1)(x + 5) + 2

    = 4x² - 12x + 9 - x² - 6x - 5 + 2 = 3x² - 18x + 6 = 3(x² - 6x + 2)

    = 3[(x - 3)² - 7] ≥ 3.(-7) = -21

Dấu "=" xảy ra khi x - 3 = 0 ⇔ x = 3. Vậy MinA = -21 ⇔ x = 3

2) B = n⁴ - 27n² + 121 = n⁴ + 22n² + 121 - 49n²

    = (n² + 11)² - (7n)² = (n² + 7n + 11)(n² - 7n + 11)

Vì n ∈ N nên n² -7n + 11 là số tự nhiên lớn hơn 1

Điều kiện cần để B là số nguyên tố là:

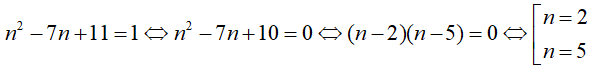
- Với n = 2 thì B = 29 (là số nguyên tố)

- Với n = 5 thì B = 71 (là số nguyên tố)

Vậy n ∈ {2, 5} là các giá trị cần tìm.

Phòng Giáo dục và Đào tạo .....

Đề khảo sát chất lượng Giữa kì 1

Năm học 2024

Môn: Toán 8

Thời gian làm bài: 90 phút

(Đề thi số 4)

Bài 1: Thực hiện các phép tính:

a) -7x²(3x - 4y)           b) (x - 3)(5x - 4)

c) (2x - 1)²           d) (x + 3)(x - 3)

Bài 2: Phân tích đa thức thành nhân tử:

a) 2x³ - 3x²      b) x² + 5xy + x + 5y      c) x² - 36 + 4xy + 4y²

Bài 3: Tìm, biết: x² - 5x + 6 = 0

Bài 4: Có 10 túi đựng tiền vàng hình dạng giống hệt nhau. Trong đó, có một túi đựng tiền giả. Những đồng tiền giả nhẹ hơn một gam so với đồng tiền thật nặng 10 gam. Bằng một chiếc cân đồng hồ và với chỉ một lần cân, hãy tìm ra túi đựng tiền giả?

Bài 5: Cho ΔABC vuông tại C (AC < BC), gọi I là trung điểm của AB. Kẻ IE ⊥ BC tại E, kẻ IF ⊥ BC tại F.

a. Chứng minh tứ giác CEIF là hình chữ nhật.

b. Gọi H là điểm đối xứng của I qua F. Chứng minh rằng tứ giác CHFE là hình bình hành.

CI cắt BF tại G, O là trung điểm của FI. Chứng minh ba điểm A, O, G thẳng hàng.

Bài 6:

Tìm các số a,b,c ∈ Q biết a² + b² + c² = ab + bc + ac và a + b + c = 2019.

Đáp án và Hướng dẫn làm bài

Bài 1:

a)

-7x²(3x - 4y)

= -7x².3x + 7x².4y

= -21x³ + 28x²y

b)

(x - 3)(5x - 4)

= x.5x - x.4 - 3.5x + 3.4

= 5x² - 4x - 15x + 12

= 5x² - 19x + 12

c)

(2x - 1)² = 4x² - 4x + 1

d)

(x + 3)(x - 3) = x² - 3² = x² - 9

Bài 2:

a) 2x³ - 3x² = x²(2x - 3)

b)

x² + 5xy + x + 5y

= x(x + 5y) + (x + 5y)

= (x + 1)(x + 5y)

c)

x² - 36 + 4xy + 4y²

= (x² + 4xy + 4y²) - 36

= (x + 2y)² - 6²

= (x + 2y - 6)(x + 2y + 6)

Bài 3:

x² - 5x + 6 = 0

x² - 2x - 3x + 6 = 0

(x² - 2x) - (3x - 6) = 0

(x - 3)(x - 2 = 0)

Trường hợp 1: x - 3 = 0 ⇒ x = 3

Trường hợp 2: x - 2 = 0 ⇒ x = 2

Vậy x ∈ {2, 3}

Bài 4:

Đánh số 10 ví theo thứ tự 1, 2, 3, ..., 10.

Lấy từ ví 1 - 1 đồng

Lấy từ ví 2 - 2 đồng

...

Lấy từ ví 10 - 10 đồng

⇒ Ta lấy được tất cả 55 đồng.

Khi đó, 55 đồng này sẽ cân nặng a gam (a > 0)

Giả sử 55 đồng này đều là tiền thật thì chúng có cân nặng là: 10.55 = 550(gam)

Mà tiền giả nhẹ hơn một gam so với tiền thật nên a < 550

Sau khi cân, thực hiện phép tính 550 - a

Nếu 550 - a = 9 thì ví 1 là ví đựng tiền giả.

Nếu 550 - a = 9.2 thì ví 2 là ví đựng tiền giả.

...

Bài 5:

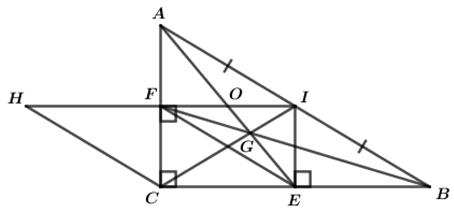
a.

Vì ΔABC vuông tại C nên ∠C = 90^o

Ta lại có: IE ⊥ BC tại E và IF ⊥ AC tại F.

⇒ ∠E = 90^o, ∠F = 90^o

Xét tứ giác IFCE ta có: ∠C = ∠E = ∠F = 90^o

⇒ Tứ giác IFCE là hình chữ nhật (dấu hiệu nhận biết).

b.

Vì tứ giác IFCE là hình chữ nhật nên IF = CE và IF // CE.

Vì H là điểm đối xứng của I qua F nên IF = HF và H, F, I thẳng hàng.

⇒ CE = HF và CE // HF

⇒ Tứ giác CHFE là hình bình hàng (dấu hiệu nhận biết hình bình hành)

c.

*) Chứng minh A, G, E thẳng hàng

Giả sử BF ∩ CI = {G}

Xét tam giác ABC ta có:

IA = IB

IF // BC

⇒ F là trung điểm AC.

Tương tự, E là trung điểm của BC

⇒ BF là đường trung tuyến của ΔABC; AE là là đường trung tuyến của ΔABC

Mà CI là là đường trung tuyến của ΔABC và BF ∩ CI = {G}

⇒ G là trọng tâm của ΔABC

⇒ A, G, E thẳng hàng (1)

*) Chứng minh A, O, E thẳng hàng

Ta có:

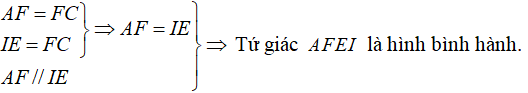
Mà O là trung điểm của IF nên O là trung điểm của AE.

⇒ A, O, E thẳng hàng (2)

Từ (1) và (2) suy ra A, O, G thẳng hàng.

Bài 6:

Theo giả thiết, ta có:

a² + b² + c² = ab + bc + ac

2(a² + b² + c²) = 2(ab + bc + ac)

2a² + 2b² + 2c² = 2ab + 2bc + 2ac

2a² + 2b² + 2c² - 2ab - 2bc - 2ac = 0

a² -2ab + b² + a² - 2ac + c² + b² - 2bc + c² = 0

(a - b)² + (a - c)² + (b - c)² = 0