Có bao nhiêu số chẵn có bốn chữ số được tạo thành từ các số 0, 1, 2, 3, 4, 5, 6

Ôn tập chương 2 (phần Đại số và Giải tích)

Bài 4 trang 76 Toán 11: Có bao nhiêu số chẵn có bốn chữ số được tạo thành từ các chữ số 0, 1, 2, 3, 4, 5, 6 sao cho:

a) Các chữ số có thể giống nhau?

b) Các chữ số khác nhau?

Trả lời

Giả sử số tạo thành là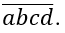

a) Vì số tạo thành các chữ số có thể lặp lại nên để đếm số các số cần tìm, ta lí luận như sau:

- Chọn chữ số hàng đơn vị: d được chọn từ các chữ số 0, 2, 4, 6. Có 4 cách chọn.

- Chọn chữ số hàng nghìn: a có 6 cách chọn từ các chữ số 1, 2,…, 6.

- Chọn chứ số hàng trăm: b được chọn từ bảy chữ số đã cho. Có 7 cách chọn.

- Chọn chữ số hàng chục: c được chọn từ bảy chữ số đã cho nên cũng có 7 cách chọn.

Từ đó theo quy tắc nhân ta có: 6.7.7.4 = 1176 (số).

b) Vì các chữ số khác nhau nên các số chẵn có 4 chữ số khác nhau tạo thành từ bảy chữ số:0, 1, 2, 3, 4, 5, 6 bao gồm:

* Các số có chữ hàng đơn vị bằng 0

Nếu d = 0 thì số cách chọn bộ ba chữ số abc là: 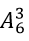= 120 (cách)

Do đó có 120 cách chọn số có bốn chữ số khác nhau mà chữ số hàng đơn vị bằng 0.

* Các số có chữ số hàng đơn vị là số chẵn khác 0

Nếu d ≠ 0 thì d có 3 cách chọn, a có 5 cách chọn.

Khi đã chọn a và d thì có: 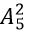= 20 cách chọn bc.

Theo quy tắc nhân, ta có số các số mà d ≠ 0 và chẵn là: 3 . 5 . 20 = 300

Vậy theo quy tắc cộng, số các số chẵn có bốn chữ số khác nhau là:

120 + 300 = 420 (số).