Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB = 12cm, AD = 16cm, AA' = 25cm
Bài tập ôn cuối năm (Phần Đại Số - Phần Hình Học)
Bài 10 trang 132 Toán 8 Tập 2: Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB = 12cm, AD = 16cm, AA' = 25cm.
a) Chứng minh rằng các tứ giác ACCA', BDD'B' là những hình chữ nhật.
b) Chứng minh rằng AC'2 = AB2 + AD2 + AA'2.
c) Tính diện tích toàn phần và thể tích của hình hộp chữ nhật.
Trả lời
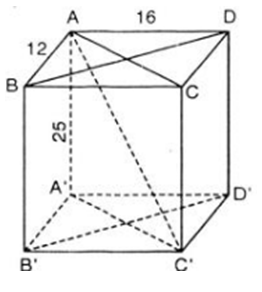
a) Do ABCD.A’B’C’D’ là hình hộp chữ nhật nên các cạnh bên bằng nhau và vuông góc với hai đáy. Do đó
AA’//CC’, AA’ = CC’, AA’ ⊥ A’C’ => ACC’A’ là hình chữ nhật
BB’//DD’, BB’ = DD’, BB’ ⊥ B’D’ => BB’D’B’ là hình chữ nhật
Ghi chú Ta có AA’ ⊄ mp(A’B’C’D’), A’C’ ⊂ mp(A’B’C’D’)
Mà AA’ ⊥ mp(A’B’C’D’) => AA’ ⊥ A’C’
Tương tự BB’ ⊥ B’D’
Chứng minh tương tự ta thấy BDD’B’ là hình chữ nhật
b) Áp dụng định lí Pi-ta-go ta có
Tam giác AA’C’ vuông tại A’ => AC’2 = A’C’2 + AA’2 (1)
Tam giác B’A’C’ vuông tại B’ => A’C’2 = A’B’2 + B’C’2 (2)
Thay vào (1) ta có AC’2 = A’B’2 + B’C’2 + AA’2
Thay A’B’ = AB ; B’C’ = A’D’ = AD vào (2) ta được :
AC’2 = AB2 + AD2 + AA’2 (đpcm)
c) Diện tích toàn phần hình hộp chữ nhật
Stp = 2(AB + AD) .AA’ + 2(AB.AD)
= 2(12+16).25 + 2.12.16 = 1784 ( cm2)
Thể tích hình hộp chữ nhật
V = AB x AD x AA' = 12.16.25 = 4800 ( cm3)

