Cho hình bình hành ABCD. Các điểm M, N theo thứ tự là trung điểm của AB, CD

Bài tập ôn cuối năm (Phần Đại Số - Phần Hình Học)

Bài 4 trang 132 Toán 8 Tập 2: Cho hình bình hành ABCD. Các điểm M, N theo thứ tự là trung điểm của AB, CD. Gọi E là giao điểm của AN và DM, K là giao điểm BN và CM. Hình bình hình ABCD phải có điều kiện gì để tứ giác MENK là:

a) Hình thoi? ;

b) Hình chữ nhật? ;

c) Hình vuông?

Trả lời

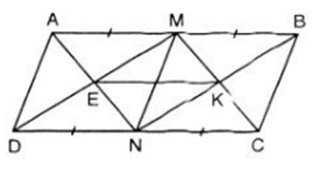
Do AB // CD và AB = CD => BM // DN và BM = DN

⇒ BMDN là hình bình hành => ME // NK (1)

Tương tự AMCN là hình bình hành => MK // NE (2)

Từ (1) và (2) suy ra MENK là hình bình hành

Tương tự các tứ giác AMND, BMNC là hình bình hành

Suy ra MN // AD và MN = AD (3)

Và E là trung điểm của MD, K là trung điểm của MC nên EK là đường trung bình của tam giác NAB

Suy ra EK // AB và EK = 1/2 AB (4)

a) Hình bình hành MENK trở thành hình thoi khi và chỉ khi MN ⊥ EK

Từ (3) và (4) suy ra AB ⊥ AD lúc đó ABCD là hình chữ nhật

Vậy ABCD là hình chữ nhật thì MENK là hình thoi

b) Hình bình hành MENK trở thành hình chữ nhật khi MN = EK

Từ (3) và (4) suy ra AD = 1/2 AB

Vậy khi hình bình hành ABCD có một cạnh gấp đôi cạnh kề nó thì MENK là hình chữ nhật

c) Kết hợp kết quả của a) và b) ta có

Nếu ABCD là hình chữ nhật có một cạnh gấp đôi cạnh kề nó thì MENK là hình vuông