Tam giác ABC có các đường cao BD, CE cắt nhau tại H

Bài tập ôn cuối năm (Phần Đại Số - Phần Hình Học)

Bài 3 trang 131 Toán 8 Tập 2: Tam giác ABC có các đường cao BD, CE cắt nhau tại H. Đường vuông góc với AB tại B và đường vuông góc với AC tại C cắt nhau ở K. Tam giác ABC phải có điều kiện gì thì tứ giác BHCK là:

a) Hình thoi?

b) Hình chữ nhật?

Trả lời

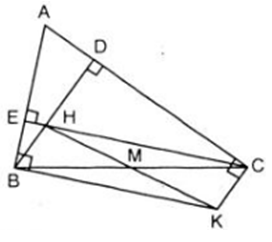
Ta có BH // KC ( vì cùng vuông góc với AC) (1)

CH // KB ( vì cùng vuông góc với AB) (2)

Từ (1) và (2) suy ra BHCK là hình bình hành

a) Hình bình hành BHCK trở thành hình thoi khi và chỉ khi HB = HC

⇔ Tam giác ABC cân tại A

Vậy tam giác ABC cân tại A thì hình bình hành BHCK trở thành hình thoi

b) Hình bình hành BHCK trở thành hình chữ nhật khi và chỉ khi nó có một góc vuông chẳng hạn ∠K = 90º

Lúc đó ∠A = 360º – (∠B+ ∠C + ∠K) = 360º – ( 90º + 90º + 90º) = 90º

Do đó tam giác ABC vuông tại A

Vậy tam giác ABC vuông tại A thì hình bình hành BHCK trở thành hình chữ nhật lúc đó điểm H trùng với điểm A.