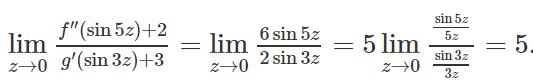Xác định b, c, d sao cho đồ thị (C) đi qua các điểm (1; 3), (−1; −3) và f′(1/3) = 5/3

Ôn tập chương 5

Bài 5.121 trang 218 Sách bài tập Đại số 11: Cho các hàm số

f(x) = x³ + bx² + cx + d (C)

g(x) = x² − 3x − 1.

a) Xác định b, c, d sao cho đồ thị (C) đi qua các điểm (1; 3), (−1; −3) và f′(1/3) = 5/3 ;

b) Viết phương trình tiếp tuyến của (C) tại điểm có hoành độ x₀ = 1;

c) Giải phương trình f′(sint) = 3;

d) Giải phương trình f′′(cost) = g′(sint);

e) Tìm giới hạn

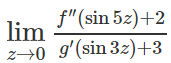
Lời giải:

a) c = 2, b = −1, d = 1 ⇒ f(x) = x³ − x² + 2x + 1;

b) f′(x) = 3x² − 2x + 2 ⇒ f′(1) = 3.

Phương trình tiếp tuyến tại M(1;3) là: y – 3 = 3(x − 1) hay y = 3x.

c) f′(sint) = 3sin²t − 2sint + 2.

f′(sint) = 3

⇔ 3sin²t − 2sint – 1 = 0

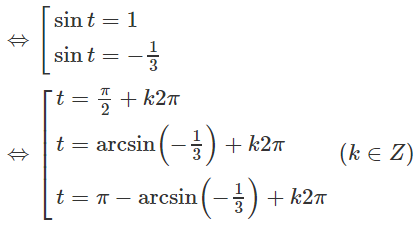
d) f′′(x) = 6x – 2 ⇒ f′′(cost) = 6cost – 2;

g′(x) = 2x – 3 ⇒ g′(sint) = 2sint − 3.

Vậy

6cost – 2 = 2sint – 3 ⇔ 2sint − 6cost = 1 ⇔ sint − 3cost = 1/2.

Đặt tanφ = 3, ta được

sin(t − φ) = cosφ/2 = α. Suy ra

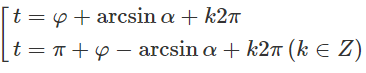
e)