Trong các dãy số (Un) sau đây, dãy số nào là cấp số cộng

Bài 3: Cấp số cộng

Bài 3.19 trang 124 Sách bài tập Đại số 11: Trong các dãy số (u_n) sau đây, dãy số nào là cấp số cộng?

 a) u_n = 3n − 1;

 b) u_n = 2ⁿ + 1;

 c) u_n = (n+1)² − n²;

 d)

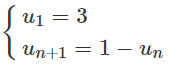
Lời giải:

 a) u_n+1 − u_n = 3(n + 1) − 1 − 3n + 1 = 3

 Vì u_n+1 = u_n + 3 nên (u_n) dãy số là cấp số cộng với u₁ = 2, d = 3.

 b) u_n+1 − u_n = 2ⁿ⁺¹ + 1 − 2ⁿ − 1 = 2ⁿ. Vì 2ⁿ không là hằng số nên dãy số (uⁿ) không phải là cấp số cộng.

 c) Ta có u_n = 2n + 1.

 Vì u_n+1 − u_n = 2(n + 1) + 1 − 2n − 1 = 2, nên dãy đã cho là cấp số cộng với u₁= 3; d = 2.

 d) Để chứng tỏ (un) không phải là cấp số cộng, ta chỉ cần chỉ ra, chẳng hạn u₃ − u₂ ≠ u₂ − u₁ là đủ.