Tìm x từ phương trình 2 + 7 + 12 + ... + x = 245, biết 2, 7, 12, ..., x là cấp số cộng

Bài 3: Cấp số cộng

Bài 3.23 trang 124 Sách bài tập Đại số 11: Tìm x từ phương trình

a) 2 + 7 + 12 + ... + x = 245, biết 2, 7, 12, ..., x là cấp số cộng.

b) (2x + 1) + (2x + 6) + (2x + 11) + ... + (2x + 96) = 1010 biết 1, 6, 11, ... là cấp số cộng.

Lời giải:

Ta có

u₁ = 2, d = 5, S_n = 245.

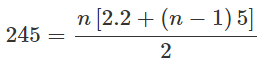
⇔5n₂ − n − 490 = 0.

Giải ra được n = 10

Từ đó tìm được x = u₁₀ = 2 + 9.5 = 47

b) Xét cấp số cộng 1, 6, 11, ..., 96.

Ta có: 96 = 1 + 5(n − 1) ⇒ n = 20

Suy ra

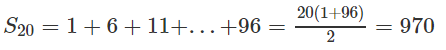
Và 2x.20 + 970 = 1010

Từ đó x = 1