Cho tứ diện ABCD. Gọi G1, G2, G3 lần lượt là trọng tâm các tam giác ABC, ACD, ABD

Bài 4: Hai mặt phẳng song song

Bài 2.22 trang 76 Sách bài tập Hình học 11: Cho tứ diện ABCD. Gọi G₁, G₂, G₃ lần lượt là trọng tâm các tam giác ABC, ACD, ABD. Chứng minh rằng (G₁G₂G₃) // (BCD).

Lời giải:

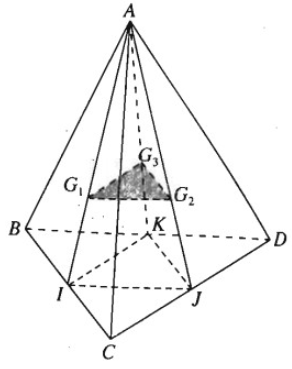
Gọi I, J và K lần lượt là trung điểm của các cạnh BC, CD và BD. Theo tính chất trọng tâm của tam giác ta có:

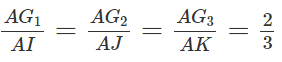
⇒ G₁G₂ // IJ

IJ ⊂ (BCD) ⇒ G₁G₂ // (BCD)

Tương tự ta có G₂G₃ // (BCD)

G₁G₂, G₂G₃ ⊂ (G₁G₂G₃)

Vậy: (G₁G₂G₃) // (BCD).