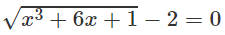Chứng minh rằng phương trình x^5 − 3x − 7 = 0 luôn có nghiệm

Bài 3: Hàm số liên tục

Bài 4.39 trang 171 Sách bài tập Đại số 11: Chứng minh rằng phương trình

a) x⁵ − 3x − 7 = 0 luôn có nghiệm;

b) cos2x = sinx − 2 có ít nhất hai nghiệm trong khoảng

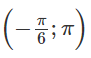
c) có nghiệm dương.

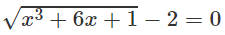
Lời giải:

a) Xét f(x) = x⁵ − 3x − 7 và hai số 0; 2.

b) Xét f(x) = cos2x - sinx + 2 trên các khoảng

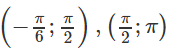
c) Ta có

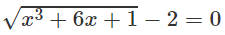
⇔ x³ + 6x + 1 = 4

⇔ x³ + 6x – 3 = 0

Hàm số f(x) = x³ + 6x − 3 liên tục trên R nên liên tục trên đoạn [0; 1] (1)

Ta có f(0). f(1) = −3. 4 < 0 (2)

Từ (1) và (2) suy ra phương trình x³ + 6x − 3 = 0 có ít nhất một nghiệm thuộc (0; 1)

Do đó, phương trình có ít nhất một nghiệm dương.