Trong mặt phẳng tọa độ Oxy, cho điểm M(3; -5), đường thẳng d có phương trình 3x + 2y – 6 = 0

Bài 3: Phép đối xứng trục

Bài 1.6 trang 16 Sách bài tập Hình học 11: Trong mặt phẳng tọa độ Oxy, cho điểm M(3; -5), đường thẳng d có phương trình 3x + 2y – 6 = 0 và đường tròn (C) có phương trình x² + y² − 2x + 4y – 4 = 0. Tìm ảnh của M, d, và (C) qua phép đối xứng qua trục Ox

Lời giải:

Gọi M′, d′ và (C') theo thứ tự là ảnh của M, d và (C) qua phép đối xứng qua trục Ox . Khi đó M′ = (3;5) . Để tìm ta viết biểu thức tọa độ của phép đối xứng qua trục:

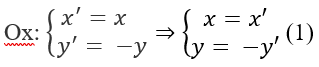
Thay (1) vào phương trình của đường thẳng d ta được 3x′ − 2y′ − 6 = 0. Từ đó suy ra phương trình của d' là 3x − 2y – 6 = 0

Thay (1) vào phương trình của (C) ta được x′² + y′² − 2x′ + 4y′ − 4 = 0 . Từ đó suy ra phương trình của (C') là (x − 1)² + (y − 2)² = 9.

Cũng có thể nhận xét (C) có tâm là I(1; −2), bán kính bằng 3, từ đó suy ra tâm I' của (C') có tọa độ (1;2) và phương trình của (C') là (x − 1)² + (y − 2)² = 9