Chọn mệnh đề đúng trong các mệnh đề sau: trang 175 SBT Đại số 11

---

Ôn tập chương 4

Bài tập trắc nghiệm trang 175, 176 Sách bài tập Đại số 11:

Bài 4.62: Chọn mệnh đề đúng trong các mệnh đề sau:

A. Nếu lim|u_n| = +∞ thì lim u_n = +∞;

B. Nếu lim|u_n| = +∞ thì lim u_n = −∞;

C. Nếu lim u_n = 0 thì lim|u_n| = 0;

D. Nếu lim u_n = −a thì lim|u_n| = a.

Lời giải:

Cách 1: Ta có ||u_n|| = |u_n|. Do đó, nếu (u_n) có giới hạn là 0 thì (|u_n|) cũng có giới hạn 0.

Cách 2: (loại trừ các phương án khác bằng cách phản ví dụ): Chẳng hạn, u_n = -n cho phép loại trừ phương án A, u_n = n cho phép loại trừ phương án B, u_n = 1 và a = -1 cho phép loại trừ phương án D.

Chọn đáp án: C

Bài 4.63: bằng:

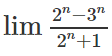
A. 1          B. -∞          C. 0          D. +∞

Lời giải:

Tính giới hạn bằng cách chia tử số và mẫu số cho 3ⁿ.

Chọn đáp án: B

Bài 4.64: bằng:

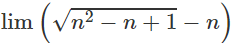
A. 0          B. 1          C. -1/2          D. -∞

Lời giải:

Tính giới hạn bằng cách nhân và chia biểu thức liên hợp.

Chọn đáp án: C

Bài 4.65: bằng:

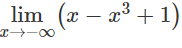
A. 1          B. -∞          C. 0          D. +∞

Lời giải:

Tính trực tiếp giới hạn.

Chọn đáp án: D

Bài 4.66: bằng:

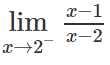
A. -∞          B. 1/4          C. 1          D. +∞

Lời giải:

Chọn đáp án: A

Bài 4.67: Cho hàm số . bằng:

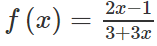
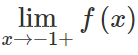
A. +∞          B. 2/3          C. 1          D. -∞

Lời giải:

Chọn đáp án: D

Bài 4.68: bằng:

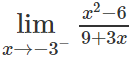
A. 1/3          B. -∞          C. 1/6          D. +∞

Lời giải:

Chọn đáp án: B

Bài 4.69: bằng:

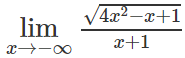
A. 2          B. -2          C. 1          D. -1

Lời giải:

Đưa x² ra khỏi căn ở tử số.

Chọn đáp án: B

Bài 4.70: Cho hàm số f(x) xác định trên đoạn [a; b]

Trong các mệnh đề sau, mệnh đề nào đúng?

A. Nếu hàm số f(x) liên tục trên đoạn [a; b] và f(a).f(b) > 0 thì phương trình f(x) = 0 không có nghiệm trong khoảng (a; b)

B. Nếu f(a).f(b) < 0 thì phương trình f(x) = 0 có ít nhất một nghiệm trong khoảng (a; b)

C. Nếu phương trình f(x) = 0 có nghiệm trong khoảng (a; b) thì hàm số f(x) phải liên tục trên khoảng (a; b)

D. Nếu f(x) hàm số liên tục, tăng trên đoạn [a; b] và f(a).f(b) < 0 thì phương trình f(x) = 0 không thể có nghiệm trong khoảng (a; b)

Lời giải:

Chọn đáp án: D

Bài 4.71: Cho phương trình 2x⁴ - 5x² + x + 1 = 0. (1)

Trong các mệnh đề sau, mệnh đề nào đúng ?

A. Phương trình (1) không có nghiệm trong khoảng (-1; 1);

B. Phương trình (1) không có nghiệm trong khoảng (-2; 0);

C. Phương trình (1) chỉ có một nghiệm trong khoảng (-2; 1) ;

D. Phương trình (1) cóít nhất hai nghiệm trong khoảng (0; 2)

Lời giải:

Đặt f(x) = 2x⁴ - 5x² + x + 1. Tính f(-1), f(0), f(1), f(2) và nhận xét dấu của chúng để kết luận.

Chọn đáp án: D