Có 7 người khách dưới sân ga lên một đoàn tàu 6 toa. Nếu số khách này lên tàu một cách

Bài 2: Hoán vị - Chỉnh hợp - Tổ hợp

Bài 2.27: Có 7 người khách dưới sân ga lên một đoàn tàu 6 toa. Nếu số khách này lên tàu một cách tùy ý thì số cách lên tàu là:

A. 6!          B. 7!

C. 6⁷          D. 7⁶

Lời giải:

Mỗi người khách có 6 cách chọn toa nên số cách lên tàu tùy ý (theo quy tắc nhân) là 6.6.6.6.6.6.6 = 6⁷.

Chọn đáp án: C

Bài 2.28: Có 7 người khách dưới sân ga lên một đoàn tàu 6 toa. Nếu toa đầu lên 2 khách, số khách còn lại mỗi người lên một toa tàu khác thì số khách lên tàu là:

Lời giải:

Có C₇² cách chọn 2 khách lên toa đầu, 5 khách còn lại mỗi người lên một trong 5 toa còn lại nên có 5! cách. Do đó đáp án đúng là C₇².5! cách.

Chọn đáp án: A

Bài 2.29: Một lớp học có 30 học sinh, trong đó có 20 học sinh nam và 10 học sinh nữ. Số cách bầu một ban cán sự lớp 4 người, trong đó có ít nhất một học sinh nam là:

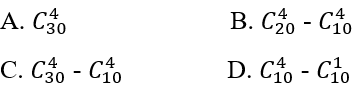
Lời giải:

Số cách bầu một ban cán sự 4 người bất kì là C₃₀⁴, số cách bầu một ban cán sự toàn nữ là C₁₀⁴. Do đó số cách bầu một ban cán sự 4 người có ít nhất 1 nam là C₃₀⁴ - C₁₀⁴.

Chọn đáp án: C

Bài 2.30: Một đội văn nghệ gồm 20 người trong đó có ba người tên là Thu, Xuân, Thắm. Số cách chọn ra một nhóm 4 người, sao cho trong đó có Thu và Xuân hoặc Thu và Thắm là:

Lời giải:

Chọn ra 4 người có Thu và Xuân trong 20 người có C₁₈² cách.

Chọn ra 4 người có Thu và Thắm trong 20 người có C₁₈² cách.

Số cách chọn 4 người có cả Thu – Xuân – Thắm trong 20 người là C₁₇¹ cách.

Vậy số cách chọn ra 4 người có Thu và Xuân hoặc Thu và Thắm là

C₁₈² + C₁₈² - C₁₇¹ = 2.C₁₈² - C₁₇¹.

Chọn đáp án: B

Bài 2.31: Cho hai đường thẳng (d) và (d') song song với nhau, trên (d) có 10 điểm và (d') có 12 điểm. Số tam giác tạo bởi các điểm trên hai đường thẳng đó là:

Lời giải:

Số tam giác có 1 đỉnh thuộc (d) và 2 đỉnh thuộc (d’) là 10.C₁₂², số tam giác có 1 đỉnh thuộc (d’) và 2 đỉnh thuộc (d) là 12.C₁₀².

Do đó số tam giác tạo được bởi các điểm trên hai đường thẳng đó là

10.C₁₂² + 12.C₁₀² = 1200 tam giác.

Chọn đáp án: D