Chứng minh các bất đẳng thức sau: a) tanx > x

Câu hỏi và bài tập ôn tập chương 1

Haylamdo biên soạn và sưu tầm lời giải Bài 68 trang 61 sgk Giải Tích 12 nâng cao được biên soạn lời giải chi tiết sẽ giúp bạn biết cách làm bài tập môn Toán 12.

Bài 68 (trang 61 sgk Giải Tích 12 nâng cao): Chứng minh các bất đẳng thức sau:

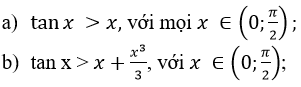
Lời giải:

a) Xét hàm số f(x) = tan x – x

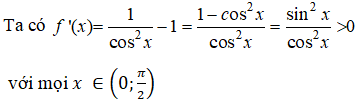
Do đó hàm số f(x) đồng biến trên (0; π/2)

Nên f(x) là hàm số đồng biến trên khoảng (0;π/2)

Vì f(0) = 0, nên khi x > 0 và x ∈ (0;π/2) thì f(x) > f(0), tức là tan x – x > 0 hay tan x > x.

b) Xét hàm số

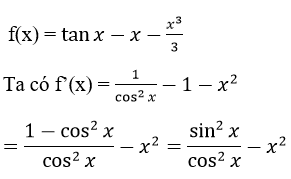
= tan²⁡x-x²⁡=(tan⁡x-x)(tan⁡x+x)>0 với mọi x ∈(0;π/2) và do câu a.

(Vì trên (0;π/2) thì tanx > 0 và x > 0 nên tanx + x > 0 .

Lại theo câu a, trên khoảng (0;π/2) thì tanx – x > 0

Do đó, (tanx + x). (tanx – x) > 0 ).

Suy ra f(x) là hàm số đồng biến trên khoảng (0;π/2)

Vì f(0) = 0 nên khi x > 0 thì f(x) > f(0), tức là tan⁡x-x-x^3/3>0 hay tan⁡x > x+x³/3 với x ∈(0;π/2)