Cho hàm số y = x - 4m/2 (mx - 1)

Câu hỏi và bài tập ôn tập chương 1

Haylamdo biên soạn và sưu tầm lời giải Bài 77 trang 63 sgk Giải Tích 12 nâng cao được biên soạn lời giải chi tiết sẽ giúp bạn biết cách làm bài tập môn Toán 12.

Bài 77 (trang 63 sgk Giải Tích 12 nâng cao): Cho hàm số

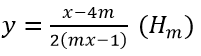
a) Khảo sát sự biến thiên và vẽ đồ thị hàm số với m = 1

b) Chứng minnh rằng với mọi m ≠ 1/2, các đường cong (H_m) đều đi qau hai điểm cố định A, B.

c) Chứng minh rằng tích các hệ số góc của tiếp tuyến với (H_m) tại hai điểm A và B là một hằng số khi m biến thiên.

Lời giải:

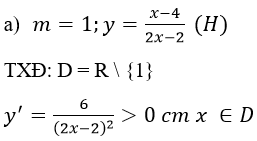
Nên hàm số đồng biến trên các khoảng (-∞;1) và (1; +∞)

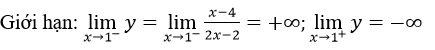
Do đó đường thẳng x = 1 là tiệm cận đứng.

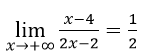
=> đường thẳng y=1/2 là tiệm cận ngang.

Bảng biến thiên

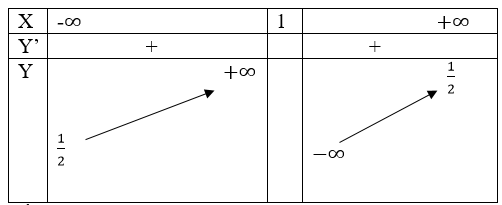
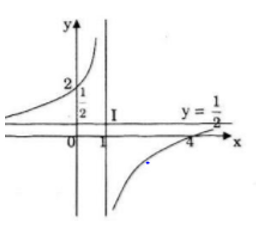
Đồ thị

Cặt trục tung tại (0; 2)

Cặt trục hoành tại (4; 0)

Đk: mx ≠ 1

b) Gọi A(x, y) là điểm cố định của đồ thị hàm số khi m thay đổi.

Khi đó tọa độ của A thỏa mãn Phương trình sau ∀m:

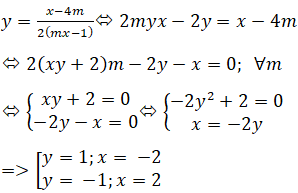
Vậy ∀m ≠ ±1/2 đồ thị hàm số luôn đi qua hai điểm cố định A(-2; 1), B(2; -1)

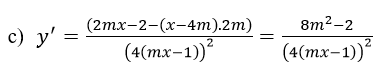
Hệ số của tiếp tuyến với (H_m) tại điểm A là y’(2), tại điểm B là y’(2)

Ta có :

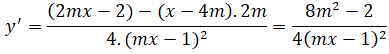
Hệ số của tiếp tuyến với (H_m) tại điểm A là y’( -2), tại điểm B là y’(2)

Ta có:

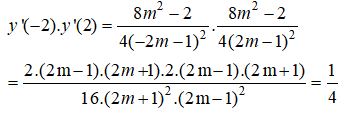
Vậy tích các hệ số góc của các tiếp tuyến với (H_m) tại 2 điểm A và B là 1 hằng số khi m biến thiên.