Cho hàm số y = f(x) = x + 1/x a) Khảo sát và vẽ đồ thị (C) của hàm số

Câu hỏi và bài tập ôn tập chương 1

Haylamdo biên soạn và sưu tầm lời giải Bài 79 trang 63 sgk Giải Tích 12 nâng cao được biên soạn lời giải chi tiết sẽ giúp bạn biết cách làm bài tập môn Toán 12.

Bài 79 (trang 63 sgk Giải Tích 12 nâng cao): Cho hàm số

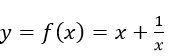
a) Khảo sát và vẽ đồ thị (C) của hàm số.

b) Tiếp tuyến của đường cong (C) tại M(x₀,y₀) cắt tiệm cận đứng và tiệm cận xiên tại hai điểm A, B. chứng minh rằng M là trung điểm trên đường cong (C).

Lời giải:

a) TXĐ: D = R \ {0}

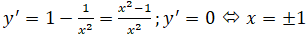
Hàm số đồng biến trên các khoảng (-∞;-1)và (1; +∞), nghịch biến trên (-1; 0) và (0; 1)

Hàm số đạt cực đại tại x = -1 và y_CĐ=y(-1)=-2

Hàm số đạt cực tiểu tại x = 1 và y_CT=y(1)=2

Giới hạn:

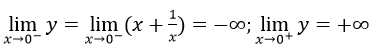
Vậy đường thẳng x = 0 là tiệm cận đứng.

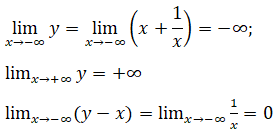
nên đường thẳng y = x là tiệm cận xiên.

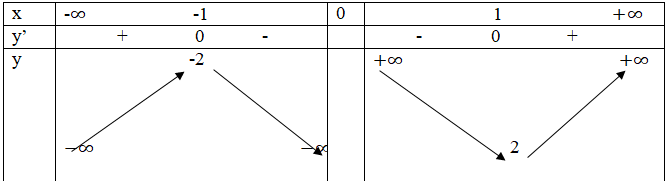
Bảng biến thiên

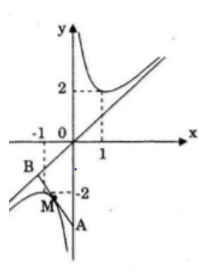
Đồ thị

b) Phương trình tiếp tuyến tại điểm M(x₀;y₀) thuộc (C) là:

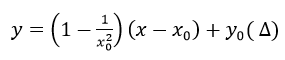
Δ cắt tiệm cận đứng tại A.

=> Tọa độ A(0;2/x₀ )

Δ cắt tiệm cận xiên tại B.

=> Tọa độ B(2x₀,2x₀)

+ Tọa độ trung điểm của AB là:

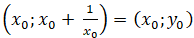
Vậy M là trung điểm của đoạn AB.

+ Khoảng cách từ B đến trục Oy bằng 2x₀ là độ dài đường cao kẻ từ B của OAB, OA có độ dài bằng 2/x₀ .

Vậy diện tích tam giác OAB là (1/2).2x₀.(2/x₀) =2 không đổi (không phụ thuộc vào vị trị của M ∈(C).