Vẽ đồ thị (T) của hàm số y=x^2-x+1 và đồ thị (H) của hàm số

Câu hỏi và bài tập ôn tập chương 1

Haylamdo biên soạn và sưu tầm lời giải Bài 78 trang 63 sgk Giải Tích 12 nâng cao được biên soạn lời giải chi tiết sẽ giúp bạn biết cách làm bài tập môn Toán 12.

Bài 78 (trang 63 sgk Giải Tích 12 nâng cao):

a) Vẽ đồ thị (T) của hàm số y=x^2-x+1 và đồ thị (H) của hàm số

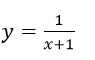
b) Tìm giao điểm của hai đường cong (T) và (H). chứng minh rằng hai đường cong đó có tiếp tuyến chung tại giao điểm chung của chúng.

c) Xác định các khoảng trên đó (H) nằm phía trên hoặc dưới (H).

Lời giải:

a) Đồ thị

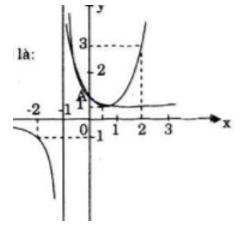
b) Cách 1. Dựa vào đồ thị ta có giao điểm của (T) và (H) là A(0; 1)

Cách 2. Hoành độ giao điểm của (T) và (H) là nghiệm của phương trình.

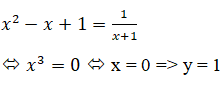
Vậy giao điểm của (T) và (H) là A(0; 1)

Phương trình tiếp tuyến của (T) tại A(0; 1) là:

y-1 = y'(0)(x-0)

⇔ y-1=-x ⇔ y=-x+1

(với y’(0) = 2.0 – 1 = -1)

Phương trình tiếp tuyến của (H) tại A(0; 1) là:

y-1 = y(0)(x-0) = -x ⇔ y = -x+1

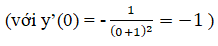
Vậy hai đường cong đó có tiếp tuyến chung tại giao điểm của chúng.

c) Cách 1. Dựa vào đồ thị ta thấy trên (-∞; -1) và (0; +∞), (P) nằm trên (H), trên (-1; 0) thì (P) nằm phía dưới (H).

Cách 2. Xét bất phương trình:

⇔ x ∈(-∞,-1)và(0; +∞), (P) nằm phía trên (H),

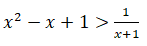
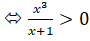
Trên (-1; 0), (P) nằm phía dưới (H).