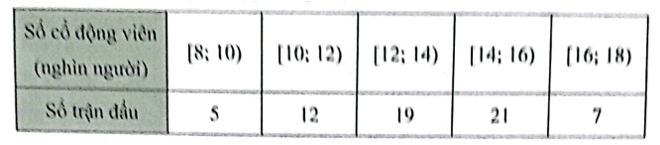
Trong một giải bóng đá, số cổ động viên đến sân cổ vũ mỗi trận đấu được ghi lại ở bảng sau

Trong một giải bóng đá, số cổ động viên đến sân cổ vũ mỗi trận đấu được ghi lại ở bảng sau (đơn vị: nghìn người):

Giải SBT Toán 12 Chân trời sáng tạo Bài tập cuối chương 3

Bài 1 trang 106 SBT Toán 12 Tập 1: Trong một giải bóng đá, số cổ động viên đến sân cổ vũ mỗi trận đấu được ghi lại ở bảng sau (đơn vị: nghìn người):

a) Khoảng biến thiên (đơn vị: nghìn người) của mẫu số liệu ghép nhóm trên là:

A. 2.

B. 8.

C. 10.

D. 18.

Lời giải:

Đáp án đúng là: C

Khoảng biến thiên của mẫu số liệu ghép nhóm trên là: 18 – 8 = 10 (nghìn người).

b) Nhóm chứa tứ phân vị thứ nhất của mẫu số liệu ghép nhóm trên là:

A. [8; 10).

B. [10; 12).

C. [12; 14).

D. [14; 16).

Lời giải:

Đáp án đúng là: B

Cỡ mẫu là: n = 5 + 12 + 19 + 21 + 7 = 64.

Ta có: $\frac{n}{4} = \frac{64}{4} = 16$ .

Tứ phân vị thứ nhất của mẫu số liệu gốc là x₁₆ ∈ [10; 12).

c) Khoảng tứ phân vị của mẫu số liệu ghép nhóm trên gần nhất với giá trị nào dưới đây?

A. 2,48.

B. 4,93.

C. 3,31.

D. 5,11.

Lời giải:

Đáp án đúng là: C

Ta có: $\frac{n}{4} = \frac{64}{4} = 16$ .

Tứ phân vị thứ nhất của mẫu số liệu gốc là x₁₆ ∈ [10; 12).

Do đó, Q₁ = 10 + $\frac{16 - 5}{12} (12 - 10)$ = 12.

Ta có: $\frac{3 n}{4} = \frac{3.64}{4} = 48$ .

Tứ phân vị thứ ba của mẫu số liệu gốc là x₄₈ ∈ [14; 16).

Do đó, Q₃ = 14 + $\frac{48 - (5 + 12 + 19)}{21} (16 - 14)$ = $\frac{106}{7}$ .

Khoảng tứ phân vị của mẫu số liệu ghép nhóm trên là:

∆Q = Q₃ – Q₁ = $\frac{106}{7}$ − 12 ≈ 3,143.

Vậy khoảng tứ phân vị của mẫu số liệu ghép nhóm trên gần nhất với giá trị 3,31.

d) Độ lệch chuẩn của mẫu số liệu ghép nhóm trên gần nhất với giá trị nào dưới đây?

A. 3,66.

B. 4,89.

C. 13,40.

D. 2,21.

Lời giải:

Đáp án đúng là: D

Số trung bình của mẫu số liệu là:

$\bar{x}$ = $\frac{9.5 + 11.12 + 13.19 + 15.21 + 17.7}{64}$ = 13,40625.

Phương sai của mẫu số liệu trên là:

s² = $\frac{9^{2} .5 + 11^{2} .12 + 13^{2} .19 + 15^{2} .21 + 17^{2} .7}{64} - 13, 40625^{2}$ ≈ 4,897.

Độ lệch chuẩn của mẫu số liệu là:

s ≈ $\sqrt{4, 897}$ ≈ 2,21.

Lời giải SBT Toán 12 Bài tập cuối chương 3 hay khác:

Xem thêm các bài giải sách bài tập Toán lớp 12 Chân trời sáng tạo hay, chi tiết khác:

❮ Bài trước Bài sau ❯