Cho y = f(x) là hàm số bậc hai có đồ thị như Hình 1. Gọi S là diện tích của hình phẳng giới hạn bởi đồ thị của hàm số y = f(x)

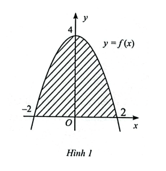
Cho y = f(x) là hàm số bậc hai có đồ thị như Hình 1. Gọi S là diện tích của hình phẳng giới hạn bởi đồ thị của hàm số y = f(x) và trục hoành.

Giải SBT Toán 12 Chân trời sáng tạo Bài tập cuối chương 4

Bài 10 trang 24 SBT Toán 12 Tập 2: Cho y = f(x) là hàm số bậc hai có đồ thị như Hình 1. Gọi S là diện tích của hình phẳng giới hạn bởi đồ thị của hàm số y = f(x) và trục hoành.

a) f(x) = 4 – 2x².

b) $S=\underset{-2}{\overset{2}{\int }}\left|f\left(x\right)\right|dx.$

c) $S=\underset{-2}{\overset{2}{\int }}f\left(x\right)dx.$

d) $S=\frac{16}{3}.$

Lời giải:

a) Quan sát đồ thị, hàm số y = f(x) = ax² + bx + c (a ≠ 0) đi qua các điểm (0; 4), (2; 0), (−2; 0).

Giải hệ phương trình:

$\left\{\begin{array}{l}a{.0}^2+b.0+c=4\\ a{.2}^2+b.2+c=0\\ a.{\left(-2\right)}^2+b.\left(-2\right)+c=0\end{array}\right.$

$\iff \left\{\begin{array}{l}c=4\\ 4a+2b=-4\\ 4a-2b=-4\end{array}\right.$

$\iff \left\{\begin{array}{l}a=-1\\ b=0\\ c=4\end{array}\right.$

Do đó y = f(x) = 4 – x².

Ta có diện tích hình phẳng đó là:

$S=\underset{-2}{\overset{2}{\int }}\left|f\left(x\right)\right|dx$

$=\underset{-2}{\overset{2}{\int }}\left|4-x^2\right|dx=\underset{-2}{\overset{2}{\int }}\left(4-x^2\right)dx$

$={\left.\left(4x-\frac{x^3}{3}\right)\right|}_{-2}^2=\frac{32}{3}$

Lời giải SBT Toán 12 Bài tập cuối chương 4 hay khác:

• Bài 1 trang 23 SBT Toán 12 Tập 2: Biết rằng f'(x) = 8x³ – 4x + 2 và f(1) = 4. Hàm số f(x) là: ....

• Bài 2 trang 23 SBT Toán 12 Tập 2: Hàm số y = f(x) có đồ thị đi qua điểm (0; 2) và f'(x) = cosx – sinx. Giá trị của f(π) là: ....

• Bài 3 trang 23 SBT Toán 12 Tập 2: Phát biểu nào sau đây đúng? ....

• Bài 4 trang 23 SBT Toán 12 Tập 2: Cho hàm số $f\left(x\right)=4\sqrt[3]{x}$. Giá trị của $\underset{1}{\overset{3}{\int }}f\left(x\right)dx-\underset{8}{\overset{3}{\int }}f\left(x\right)dx$ bằng: ....

• Bài 5 trang 23 SBT Toán 12 Tập 2: Cho hàm số f(x) = 3x – 1. Biết rằng a là số thỏa mãn $\underset{0}{\overset{1}{\int }}{f}^2\left(x\right)dx=a{\left[\underset{0}{\overset{1}{\int }}f\left(x\right)dx\right]}^2$. Giá trị của a là: ....

• Bài 6 trang 23 SBT Toán 12 Tập 2: Đồ thị của hàm số y = f(x) đi qua điểm (1; 1) và có hệ số góc của tiếp tuyến tại các điểm (x; f(x)) là 1 – 4x. giá trị của f(3) là: ....

• Bài 7 trang 24 SBT Toán 12 Tập 2: Cho hàm số f(x) liên tục trên đoạn [1; 3] và thỏa mãn $\underset{1}{\overset{3}{\int }}\left[3x^2-2f^{\text{'}}\left(x\right)\right]dx=4;f\left(1\right)=-2$. Giá trị f(3) là: ....

• Bài 8 trang 24 SBT Toán 12 Tập 2: Diện tích hình phẳng giới hạn bởi đồ thị của hàm số y = e^x – 2, trục hoành và hai đường thẳng x = 0, x = ln4 là: ....

• Bài 9 trang 24 SBT Toán 12 Tập 2: Cho K là một khoảng trên ℝ; F(x) là một nguyên hàm của hàm số f(x) trên K; G(x) là một nguyên hàm của hàm số g(x) trên K ....

• Bài 1 trang 25 SBT Toán 12 Tập 2: Tiếp tuyến của đồ thị hàm số y = f(x) tại điểm (x; f(x)) có hệ số góc là 3x² – 6x + 2. Tìm hàm số y = f(x), biết đồ thị của nó đi qua điểm (−1; 1). ....

• Bài 2 trang 25 SBT Toán 12 Tập 2: Tìm: $\int {\left(3x-\frac{1}{x^2}\right)}^{2}dx$; $\int \left(7x\sqrt[3]{x}-\frac{1}{\sqrt{x^3}}\right)dx$ (x > 0).....

• Bài 3 trang 25 SBT Toán 12 Tập 2: Tính: $\underset{1}{\overset{2}{\int }}\frac{x^4+x^3+x^2+x+1}{x^2}dx;$$\underset{1}{\overset{2}{\int }}\frac{x{e}^x+1}{x}dx$ ....

• Bài 4 trang 25 SBT Toán 12 Tập 2: Cho hàm số f(x) liên tục trên đoạn [0; 5]. Tính $\underset{0}{\overset{5}{\int }}f\left(x\right)dx$, biết rằng $\underset{0}{\overset{3}{\int }}f\left(x\right)dx=4;\underset{1}{\overset{5}{\int }}f\left(x\right)dx=6;\underset{1}{\overset{3}{\int }}f\left(x\right)dx=3.$ ....

• Bài 5 trang 25 SBT Toán 12 Tập 2: Cho hàm số y = f(x) có đồ thị như hình bên. Biết rằng đạo hàm f'(x) liên tục trên ℝ. Tính $\underset{-1}{\overset{1}{\int }}{f}^{\text{'}}\left(x\right)dx$. ....

• Bài 6 trang 25 SBT Toán 12 Tập 2: Cho hàm số f(x) liên tục trên ℝ, có đạo hàm $f^{\text{'}}\left(x\right)=\left\{\begin{array}{l}4-3x^2,x<1\\ \mathrm{1,}x\ge 1.\end{array}\right.$.Tính f(2) – f(0). ....

• Bài 7 trang 26 SBT Toán 12 Tập 2: Cho hàm số f(x) liên tục trên đoạn $\left[0;\frac{\pi }{2}\right]$ và thỏa mãn $\underset{0}{\overset{\frac{\pi }{2}}{\int }}\left[3\cos x+2f^{\text{'}}\left(x\right)\right]dx=-5;f\left(0\right)=1$. Tính giá trị $f\left(\frac{\pi }{2}\right)$ ....

• Bài 8 trang 26 SBT Toán 12 Tập 2: Cho D là hình phẳng giới hạn bởi đồ thị của đồ thị $y=\sqrt{x}$, trục hoành và đường thẳng x = 4. ....

• Bài 9 trang 26 SBT Toán 12 Tập 2: Tính thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi đồ thị của hàm số y = 1 + x² ....

• Bài 10 trang 26 SBT Toán 12 Tập 2: Một cột bê tông hình trụ có chiều cao 9 m. Nếu cắt cột bê tông bằng mặt phẳng nằm ngang cách chân cột x (m) ....

• Bài 11 trang 26 SBT Toán 12 Tập 2: Một chiếc xe đang chuyển động với vận tốc với tốc độ v₀ = 5 m/s thì tăng tốc với gia tốc không đổi x = 3 m/s² ....

• Bài 12 trang 26 SBT Toán 12 Tập 2: Giả sử tốc độ tăng trưởng của một quần thể muỗi thỏa mãn công thức N'(t) = 0,2N(t), 0 ≤ t ≤ 5 ....