Cho hàm số y = (m – 1)x^3 + 2(m + 1)x^2 – x + m – 1 (m là tham số)

Cho hàm số y = (m – 1)x + 2(m + 1)x – x + m – 1 (m là tham số)

Giải SBT Toán 12 Chân trời sáng tạo Bài 4: Khảo sát và vẽ đồ thị một số hàm số cơ bản

Bài 2 trang 31 SBT Toán 12 Tập 1: Cho hàm số y = (m – 1)x³ + 2(m + 1)x² – x + m – 1 (m là tham số)

a) Khảo sát và vẽ đồ thị của hàm số khi m = −1.

b) Tìm giá trị của m để tâm đối xứng của đồ thị hàm số có hoành độ x₀ = −2.

Lời giải:

a) Khi m = −1 ta được: y = −2x³ – x – 2.

Tập xác định: D = ℝ.

Ta có: y' = −6x² – 1

           y' = 0 phương trình vô nghiệm.

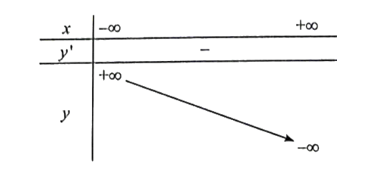
Ta có bảng biến thiên:

Hàm số nghịch biến trên ℝ.

Hàm số không cực trị.

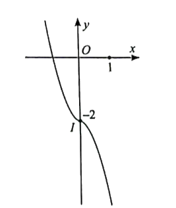
Đồ thị hàm số

b) Ta có: y = (m – 1)x³ + 2(m + 1)x² – x + m – 1               

               y' = 3(m – 1)x² + 4(m + 1)x – 1

               y'' = 6(m – 1)x + 4(m + 1).

               y'' = 0 ⇔ $\left\{\begin{array}{l}m-1\ne 0\\ x=\frac{-2\left(m+1\right)}{3\left(m-1\right)}\end{array}\right.$.

Để tâm đối xứng của đồ thị hàm số có hoành độ x₀ = −2.

⇔ $\left\{\begin{array}{l}m-1\ne 0\\ \frac{-2\left(m+1\right)}{3\left(m-1\right)}=-2\end{array}\right.$ ⇔ $\left\{\begin{array}{l}m\ne 1\\ 2m+2=6m-6\end{array}\right.$ ⇔ m = 2.

Lời giải SBT Toán 12 Bài 4: Khảo sát và vẽ đồ thị một số hàm số cơ bản hay khác:

• Bài 1 trang 31 SBT Toán 12 Tập 1: Khảo sát và vẽ đồ thị của các hàm số sau: a) y = x(x² – 4x);....

• Bài 3 trang 31 SBT Toán 12 Tập 1: Cho hàm số y = 2x³ + 6x² – x + 2. Viết phương trình tiếp tuyến của đồ thị hàm số tại tâm đối xứng của nó.....

• Bài 4 trang 31 SBT Toán 12 Tập 1: Với giá trị nào của m thì đồ thị của hàm số y = −x³ – 3x² + mx + 1 có tâm đối xứng nằm trên trục Ox?....

• Bài 5 trang 31 SBT Toán 12 Tập 1: Khảo sát và vẽ đồ thị của các hàm số sau: a) y = 3 + $\frac{1}{3}$....

• Bài 6 trang 32 SBT Toán 12 Tập 1: Ta đã biết đồ thị hàm số y = $\frac{2x-1}{x+1}$ có tiệm cận đứng là đường thẳng x = −1 và tiệm cận ngang là đường thẳng y = 2.....

• Bài 7 trang 32 SBT Toán 12 Tập 1: Cho hàm số y = $\frac{2x-1}{-x+3}$. Chứng tỏ rằng đường thẳng y = −x cắt đồ thị hàm số đã cho tại hai điểm phân biệt.....

• Bài 8 trang 32 SBT Toán 12 Tập 1: Khảo sát và vẽ đồ thị của các hàm số sau: a) $y=\frac{x^2-2x+2}{x-1}$....

• Bài 9 trang 32 SBT Toán 12 Tập 1: Cho hàm số $y=\frac{x^2+2x-2}{x-1}$ a) Tìm tọa độ giao điểm I của hai đường tiệm cận của đồ thị hàm số.....

• Bài 10 trang 32 SBT Toán 12 Tập 1: Cho hàm số y = $\frac{\left(m-1\right)x-2}{m-2-x}$ (m là tham số).....

• Bài 11 trang 32 SBT Toán 12 Tập 1: Cho hàm số y = $\frac{x^2+2x-m}{x-1}$ (m là tham số). ....