Khảo sát và vẽ đồ thị của các hàm số sau trang 31 SBT Toán 12 Tập 1

---

Khảo sát và vẽ đồ thị của các hàm số sau:

Giải SBT Toán 12 Chân trời sáng tạo Bài 4: Khảo sát và vẽ đồ thị một số hàm số cơ bản

Bài 5 trang 31 SBT Toán 12 Tập 1: Khảo sát và vẽ đồ thị của các hàm số sau:

a) y = 3 + $\frac{1}{x}$;

b) y = 2 – $\frac{1}{1+x}$.

Lời giải:

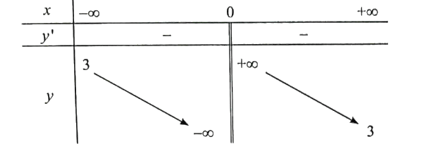
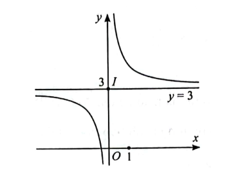
a) y = 3 + $\frac{1}{x}$

Tập xác định: D = ℝ\{0}.

Giới hạn của hàm số:

$\underset{x\to +\infty }{\lim }y=\underset{x\to +\infty }{\lim }\left(3+\frac{1}{x}\right)=3$; $\underset{x\to -\infty }{\lim }y=\underset{x\to -\infty }{\lim }\left(3+\frac{1}{x}\right)=3$.

Do đó, đồ thị hàm số có tiệm cận ngang y = 3.

$\underset{x\to 0^{+}}{\lim }y=\underset{x\to 0^{+}}{\lim }\left(3+\frac{1}{x}\right)=+\infty$; $\underset{x\to 0^{-}}{\lim }y=\underset{x\to 0^{-}}{\lim }\left(3+\frac{1}{x}\right)=-\infty$.

Do đó, đồ thị hàm số có tiệm cận đứng x = 0.

Ta có: y' = $-\frac{1}{x^2}$

           y' < 0 với mọi x ≠ 0 nên hàm số nghịch biến trên các khoảng (−∞; 0) và (0; +∞).

Ta có bảng biến thiên:

Đồ thị hàm số:

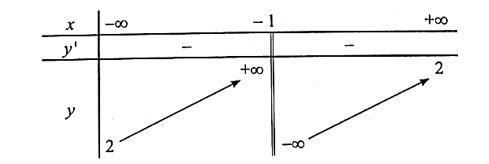
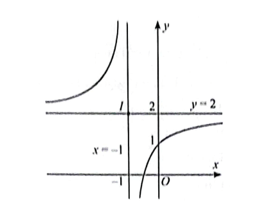
b) y = 2 – $\frac{1}{1+x}$

Tập xác định: D = ℝ\{−1}.

Giới hạn của hàm số:

$\underset{x\to +\infty }{\lim }y=\underset{x\to +\infty }{\lim }\left(2-\frac{1}{1+x}\right)=2$; $\underset{x\to -\infty }{\lim }y=\underset{x\to -\infty }{\lim }\left(2-\frac{1}{1+x}\right)=2$.

Do đó, đồ thị hàm số có tiệm cận ngang y = 2.

$\underset{x\to -1^{+}}{\lim }y=\underset{x\to -1^{+}}{\lim }\left(2-\frac{1}{1+x}\right)=-\infty$; $\underset{x\to -1^{-}}{\lim }y=\underset{x\to -1^{-}}{\lim }\left(2-\frac{1}{1+x}\right)=+\infty$.

Do đó, đồ thị hàm số có tiệm cận đứng x = −1.

Ta có bảng biến thiên:

Ta có: y' = $\frac{1}{{\left(1+x\right)}^2}$ > 0 với mọi x ≠ −1 nên hàm số đồng biến trên khoảng (−∞; −1) và (−1; +∞).

Đồ thị hàm số:

Lời giải SBT Toán 12 Bài 4: Khảo sát và vẽ đồ thị một số hàm số cơ bản hay khác:

• Bài 1 trang 31 SBT Toán 12 Tập 1: Khảo sát và vẽ đồ thị của các hàm số sau: a) y = x(x² – 4x);....

• Bài 2 trang 31 SBT Toán 12 Tập 1: Cho hàm số y = (m – 1)x³ + 2(m + 1)x² – x + m – 1 (m là tham số).....

• Bài 3 trang 31 SBT Toán 12 Tập 1: Cho hàm số y = 2x³ + 6x² – x + 2. Viết phương trình tiếp tuyến của đồ thị hàm số tại tâm đối xứng của nó.....

• Bài 4 trang 31 SBT Toán 12 Tập 1: Với giá trị nào của m thì đồ thị của hàm số y = −x³ – 3x² + mx + 1 có tâm đối xứng nằm trên trục Ox?....

• Bài 6 trang 32 SBT Toán 12 Tập 1: Ta đã biết đồ thị hàm số y = $\frac{2x-1}{x+1}$ có tiệm cận đứng là đường thẳng x = −1 và tiệm cận ngang là đường thẳng y = 2.....

• Bài 7 trang 32 SBT Toán 12 Tập 1: Cho hàm số y = $\frac{2x-1}{-x+3}$. Chứng tỏ rằng đường thẳng y = −x cắt đồ thị hàm số đã cho tại hai điểm phân biệt.....

• Bài 8 trang 32 SBT Toán 12 Tập 1: Khảo sát và vẽ đồ thị của các hàm số sau: a) $y=\frac{x^2-2x+2}{x-1}$....

• Bài 9 trang 32 SBT Toán 12 Tập 1: Cho hàm số $y=\frac{x^2+2x-2}{x-1}$ a) Tìm tọa độ giao điểm I của hai đường tiệm cận của đồ thị hàm số.....

• Bài 10 trang 32 SBT Toán 12 Tập 1: Cho hàm số y = $\frac{\left(m-1\right)x-2}{m-2-x}$ (m là tham số).....

• Bài 11 trang 32 SBT Toán 12 Tập 1: Cho hàm số y = $\frac{x^2+2x-m}{x-1}$ (m là tham số). ....