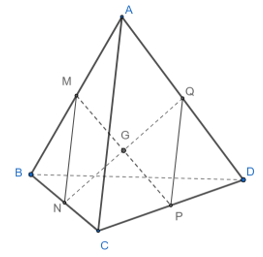
Cho tứ diện ABCD. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, DA

Giải sách bài tập Toán 12 Bài 6: Vectơ trong không gian - Kết nối tri thức

Bài 2.13 trang 46 SBT Toán 12 Tập 1: Cho tứ diện ABCD. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, DA. Gọi G là giao điểm của MP và NQ. Chứng minh rằng $\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}+\overrightarrow{GD}=\overrightarrow{0}.$

Lời giải:

Vì MN là đường trung bình của tam giác ABC nên MN // AC và MN = $\frac{1}{2}$AC.

Vì PQ là đường trung bình của tam giác ADC nên NP // AC và NP = $\frac{1}{2}$AC.

Do dó, MN //AC và MNPQ là hình bình hành.

Theo đề bài, G là giao điểm của MNPQ là hình bình hành và G là giao điểm MP và NQ nên G là trung điểm của mỗi đoạn thẳng đó.

Ta có: $\left(\overrightarrow{GA}+\overrightarrow{GB}\right)+\left(\overrightarrow{GC}+\overrightarrow{GD}\right)$ = $2\overrightarrow{GM}+2\overrightarrow{GP}$ = 2$\left(\overrightarrow{GM}+\overrightarrow{GP}\right)$ = 2.$\overrightarrow{0}$ = $\overrightarrow{0}$.

Lời giải Sách bài tập Toán lớp 12 Bài 6: Vectơ trong không gian hay khác:

• Bài 2.1 trang 43 SBT Toán 12 Tập 1: Cho hình chóp tứ giác S.ABCD. Trong các vectơ có điểm đầu và điểm cuối phân biệt ....

• Bài 2.2 trang 44 SBT Toán 12 Tập 1: Cho hình hộp ABCD.A'B'C'D'. Trong các vectơ có điểm đầu và điểm cuối là hai đỉnh phân biệt của hình hộp ....

• Bài 2.3 trang 44 SBT Toán 12 Tập 1: Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB = AD = 1 và AA' = 2. Tính độ dài của các vectơ sau: ....

• Bài 2.4 trang 44 SBT Toán 12 Tập 1: Trong không gian, cho năm điểm phân biệt A, B, C, D, E. Chứng minh rằng: ....

• Bài 2.5 trang 44 SBT Toán 12 Tập 1: Cho tứ diện ABCD. Gọi E, F là các điểm lần lượt thuộc các cạnh AB, CD ....

• Bài 2.6 trang 44 SBT Toán 12 Tập 1: Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của các cạnh BC, BD ....

• Bài 2.7 trang 44 SBT Toán 12 Tập 1: Một tòa chung cư có chiều cao của các tầng như nhau. Một thang máy di chuyển từ tầng 10 ....

• Bài 2.8 trang 45 SBT Toán 12 Tập 1: Một chiếc bàn cân đối được đặt trên mặt sàn nằm ngang, mặt bàn song song với mặt sàn ....

• Bài 2.9 trang 45 SBT Toán 12 Tập 1: Cho hình hộp ABCD.A'B'C'D'. Đặt $\overrightarrow{A{A}^{\text{'}}}=\overrightarrow{x}$, $\overrightarrow{AB}=\overrightarrow{y}$ và $\overrightarrow{AC}=\overrightarrow{z}$ ....

• Bài 2.10 trang 45 SBT Toán 12 Tập 1: Trong không gian, cho hai hình bình hành ABCD và A'B'C'D'. Chứng minh rằng: ....

• Bài 2.11 trang 45 SBT Toán 12 Tập 1: Cho hình lăng trụ đứng ABCD.A'B'C'D'. Biết rằng AA' = 2 và tứ giác ABCD ....

• Bài 2.12 trang 46 SBT Toán 12 Tập 1: Trong không gian, cho hai vectơ $\overrightarrow{\mathrm{a}}$ và $\overrightarrow{\mathrm{b}}$thỏa mãn $\left|\overrightarrow{\mathrm{a}}\right|$ = 1, $\left|\overrightarrow{\mathrm{b}}\right|$ = 2 và $\left(\overrightarrow{\mathrm{a}},\overrightarrow{\mathrm{b}}\right)$ = 45° ....

• Bài 2.14 trang 46 SBT Toán 12 Tập 1: Cho hình lập phương ABCD.A'B'C'D' có độ dài các cạnh bằng a ....

• Bài 2.15 trang 46 SBT Toán 12 Tập 1: Cho hình chóp S.ABC có SA = SB = SC và $\widehat{\mathrm{ASB}}=\widehat{\mathrm{BSC}}=\widehat{\mathrm{CSA}}$ ....