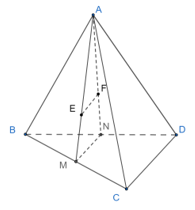
Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của các cạnh BC, BD

Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của các cạnh BC, BD. Gọi E, F lần lượt là trọng tâm của các tam giác ABC, ABD. Chứng minh rằng:

Giải sách bài tập Toán 12 Bài 6: Vectơ trong không gian - Kết nối tri thức

Bài 2.6 trang 44 SBT Toán 12 Tập 1: Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của các cạnh BC, BD. Gọi E, F lần lượt là trọng tâm của các tam giác ABC, ABD. Chứng minh rằng:

a) $\overrightarrow{EF}=\frac{2}{3}\overrightarrow{MN}$;

b) $\overrightarrow{EF}=\frac{1}{3}\overrightarrow{CD}$.

Lời giải:

a) Xét tam giác AMN, ta có: AE = $\frac{2}{3}$AM, AF = $\frac{2}{3}$AN (E, F là trọng tâm tam giác ABC, ABD).

Theo định lí Thales đảo suy EF // MN và EF = $\frac{2}{3}$MN.

Vì $\overrightarrow{EF}$ và $\overrightarrow{MN}$ cùng hướng nên $\overrightarrow{EF}=\frac{2}{3}\overrightarrow{MN}$.

b) Xét tam giác BCD, có M, N là trung điểm CB, DB nên MN là đường trung bình của tam giác.

Ta có: MN // CD và MN = $\frac{1}{2}$CD.

$\overrightarrow{CD}$ và $\overrightarrow{MN}$ cùng hướng nên $\overrightarrow{MN}=\frac{1}{2}\overrightarrow{CD}$.

Do đó, $\overrightarrow{EF}=\frac{2}{3}\overrightarrow{MN}=\frac{2}{3}.\frac{1}{2}\overrightarrow{CD}=\frac{1}{3}\overrightarrow{CD}$.

Vậy $\overrightarrow{EF}=\frac{1}{3}\overrightarrow{CD}$.

Lời giải Sách bài tập Toán lớp 12 Bài 6: Vectơ trong không gian hay khác:

• Bài 2.1 trang 43 SBT Toán 12 Tập 1: Cho hình chóp tứ giác S.ABCD. Trong các vectơ có điểm đầu và điểm cuối phân biệt ....

• Bài 2.2 trang 44 SBT Toán 12 Tập 1: Cho hình hộp ABCD.A'B'C'D'. Trong các vectơ có điểm đầu và điểm cuối là hai đỉnh phân biệt của hình hộp ....

• Bài 2.3 trang 44 SBT Toán 12 Tập 1: Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB = AD = 1 và AA' = 2. Tính độ dài của các vectơ sau: ....

• Bài 2.4 trang 44 SBT Toán 12 Tập 1: Trong không gian, cho năm điểm phân biệt A, B, C, D, E. Chứng minh rằng: ....

• Bài 2.5 trang 44 SBT Toán 12 Tập 1: Cho tứ diện ABCD. Gọi E, F là các điểm lần lượt thuộc các cạnh AB, CD ....

• Bài 2.7 trang 44 SBT Toán 12 Tập 1: Một tòa chung cư có chiều cao của các tầng như nhau. Một thang máy di chuyển từ tầng 10 ....

• Bài 2.8 trang 45 SBT Toán 12 Tập 1: Một chiếc bàn cân đối được đặt trên mặt sàn nằm ngang, mặt bàn song song với mặt sàn ....

• Bài 2.9 trang 45 SBT Toán 12 Tập 1: Cho hình hộp ABCD.A'B'C'D'. Đặt $\overrightarrow{A{A}^{\text{'}}}=\overrightarrow{x}$, $\overrightarrow{AB}=\overrightarrow{y}$ và $\overrightarrow{AC}=\overrightarrow{z}$ ....

• Bài 2.10 trang 45 SBT Toán 12 Tập 1: Trong không gian, cho hai hình bình hành ABCD và A'B'C'D'. Chứng minh rằng: ....

• Bài 2.11 trang 45 SBT Toán 12 Tập 1: Cho hình lăng trụ đứng ABCD.A'B'C'D'. Biết rằng AA' = 2 và tứ giác ABCD ....

• Bài 2.12 trang 46 SBT Toán 12 Tập 1: Trong không gian, cho hai vectơ $\overrightarrow{\mathrm{a}}$ và $\overrightarrow{\mathrm{b}}$thỏa mãn $\left|\overrightarrow{\mathrm{a}}\right|$ = 1, $\left|\overrightarrow{\mathrm{b}}\right|$ = 2 và $\left(\overrightarrow{\mathrm{a}},\overrightarrow{\mathrm{b}}\right)$ = 45° ....

• Bài 2.13 trang 46 SBT Toán 12 Tập 1: Cho tứ diện ABCD. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, DA ....

• Bài 2.14 trang 46 SBT Toán 12 Tập 1: Cho hình lập phương ABCD.A'B'C'D' có độ dài các cạnh bằng a ....

• Bài 2.15 trang 46 SBT Toán 12 Tập 1: Cho hình chóp S.ABC có SA = SB = SC và $\widehat{\mathrm{ASB}}=\widehat{\mathrm{BSC}}=\widehat{\mathrm{CSA}}$ ....