Cho tứ diện ABCD. Gọi E, F là các điểm lần lượt thuộc các cạnh AB, CD

Giải sách bài tập Toán 12 Bài 6: Vectơ trong không gian - Kết nối tri thức

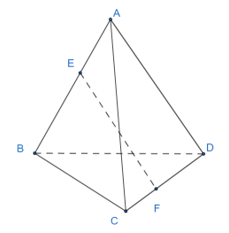
Bài 2.5 trang 44 SBT Toán 12 Tập 1: Cho tứ diện ABCD. Gọi E, F là các điểm lần lượt thuộc các cạnh AB, CD sao cho AE = $\frac{1}{3}$AB và CF = $\frac{1}{3}$CD. Chứng minh rằng:

a) $\overrightarrow{EF}=\overrightarrow{AD}-\frac{1}{3}\overrightarrow{AB}-\frac{2}{3}\overrightarrow{CD}$;

b) $\overrightarrow{EF}=\overrightarrow{BC}+\frac{2}{3}\overrightarrow{AB}+\frac{1}{3}\overrightarrow{CD}$;

c) $\overrightarrow{EF}=\frac{1}{3}\overrightarrow{AD}+\frac{2}{3}\overrightarrow{BC}+\frac{1}{3}\overrightarrow{AB}$.

Lời giải:

a) Ta có: $\overrightarrow{EF}=\overrightarrow{EA}+\overrightarrow{AD}+\overrightarrow{DF}$

                     = $-\overrightarrow{AE}+\overrightarrow{AD}-\overrightarrow{FD}$

                     = $\overrightarrow{AD}-\frac{1}{3}\overrightarrow{AB}-\frac{2}{3}\overrightarrow{CD}$.

Vậy $\overrightarrow{EF}=\overrightarrow{AD}-\frac{1}{3}\overrightarrow{AB}-\frac{2}{3}\overrightarrow{CD}$.

b) Ta có: $\overrightarrow{EF}=\overrightarrow{EB}+\overrightarrow{BC}+\overrightarrow{CF}$

                     = $\frac{2}{3}\overrightarrow{AB}+\overrightarrow{CB}+\frac{1}{3}\overrightarrow{CD}$.

Vậy $\overrightarrow{EF}=\overrightarrow{BC}+\frac{2}{3}\overrightarrow{AB}+\frac{1}{3}\overrightarrow{CD}$.

c) Từ câu a và b, ta có:

$3\overrightarrow{EF}=\left(\overrightarrow{AD}-\frac{1}{3}\overrightarrow{AB}-\frac{2}{3}\overrightarrow{CD}\right)+2\left(\frac{2}{3}\overrightarrow{AB}+\overrightarrow{CB}+\frac{1}{3}\overrightarrow{CD}\right)$

        = $\overrightarrow{AD}-\frac{1}{3}\overrightarrow{AB}-\frac{2}{3}\overrightarrow{CD}$

        = $\overrightarrow{AD}$ + $\overrightarrow{AD}-\frac{1}{3}\overrightarrow{AB}-\frac{2}{3}\overrightarrow{CD}$ + $\left(-\frac{2}{3}\overrightarrow{CD}+\frac{2}{3}\overrightarrow{CD}\right)$ + $2\overrightarrow{CB}$

        = $\overrightarrow{AD}+2\overrightarrow{CB}+\overrightarrow{AB}$

⇒ $\overrightarrow{EF}=\frac{1}{3}\overrightarrow{AD}+\frac{2}{3}\overrightarrow{BC}+\frac{1}{3}\overrightarrow{AB}$.

Vậy ta có đpcm.

Lời giải Sách bài tập Toán lớp 12 Bài 6: Vectơ trong không gian hay khác:

• Bài 2.1 trang 43 SBT Toán 12 Tập 1: Cho hình chóp tứ giác S.ABCD. Trong các vectơ có điểm đầu và điểm cuối phân biệt ....

• Bài 2.2 trang 44 SBT Toán 12 Tập 1: Cho hình hộp ABCD.A'B'C'D'. Trong các vectơ có điểm đầu và điểm cuối là hai đỉnh phân biệt của hình hộp ....

• Bài 2.3 trang 44 SBT Toán 12 Tập 1: Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB = AD = 1 và AA' = 2. Tính độ dài của các vectơ sau: ....

• Bài 2.4 trang 44 SBT Toán 12 Tập 1: Trong không gian, cho năm điểm phân biệt A, B, C, D, E. Chứng minh rằng: ....

• Bài 2.6 trang 44 SBT Toán 12 Tập 1: Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của các cạnh BC, BD ....

• Bài 2.7 trang 44 SBT Toán 12 Tập 1: Một tòa chung cư có chiều cao của các tầng như nhau. Một thang máy di chuyển từ tầng 10 ....

• Bài 2.8 trang 45 SBT Toán 12 Tập 1: Một chiếc bàn cân đối được đặt trên mặt sàn nằm ngang, mặt bàn song song với mặt sàn ....

• Bài 2.9 trang 45 SBT Toán 12 Tập 1: Cho hình hộp ABCD.A'B'C'D'. Đặt $\overrightarrow{A{A}^{\text{'}}}=\overrightarrow{x}$, $\overrightarrow{AB}=\overrightarrow{y}$ và $\overrightarrow{AC}=\overrightarrow{z}$ ....

• Bài 2.10 trang 45 SBT Toán 12 Tập 1: Trong không gian, cho hai hình bình hành ABCD và A'B'C'D'. Chứng minh rằng: ....

• Bài 2.11 trang 45 SBT Toán 12 Tập 1: Cho hình lăng trụ đứng ABCD.A'B'C'D'. Biết rằng AA' = 2 và tứ giác ABCD ....

• Bài 2.12 trang 46 SBT Toán 12 Tập 1: Trong không gian, cho hai vectơ $\overrightarrow{\mathrm{a}}$ và $\overrightarrow{\mathrm{b}}$thỏa mãn $\left|\overrightarrow{\mathrm{a}}\right|$ = 1, $\left|\overrightarrow{\mathrm{b}}\right|$ = 2 và $\left(\overrightarrow{\mathrm{a}},\overrightarrow{\mathrm{b}}\right)$ = 45° ....

• Bài 2.13 trang 46 SBT Toán 12 Tập 1: Cho tứ diện ABCD. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, DA ....

• Bài 2.14 trang 46 SBT Toán 12 Tập 1: Cho hình lập phương ABCD.A'B'C'D' có độ dài các cạnh bằng a ....

• Bài 2.15 trang 46 SBT Toán 12 Tập 1: Cho hình chóp S.ABC có SA = SB = SC và $\widehat{\mathrm{ASB}}=\widehat{\mathrm{BSC}}=\widehat{\mathrm{CSA}}$ ....