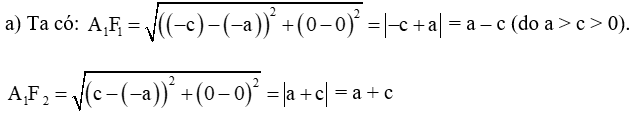Hoạt động 2 trang 94 Toán lớp 10 Tập 2 Cánh diều

Trong mặt phẳng, xét đường elip (E) là tập hợp các điểm M sao cho MF + MF = 2a, ở đó FF = 2c (với a > c > 0).

Giải Toán lớp 10 Bài 6: Ba đường conic

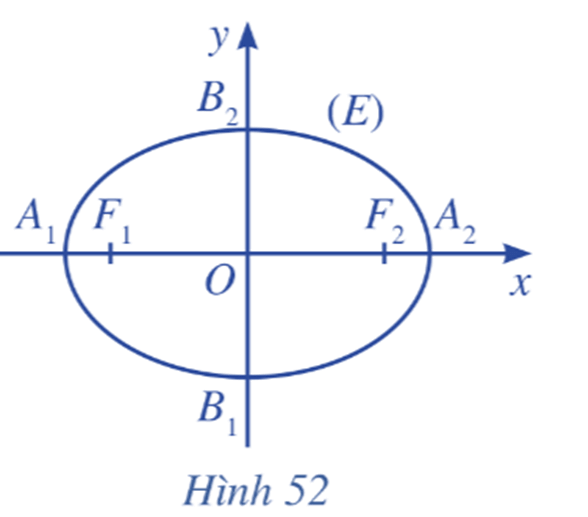
Hoạt động 2 trang 94 Toán lớp 10 Tập 2: Trong mặt phẳng, xét đường elip (E) là tập hợp các điểm M sao cho MF₁ + MF₂ = 2a, ở đó F₁F₂ = 2c (với a > c > 0).

Ta chọn hệ trục tọa độ Oxy có gốc là trung điểm của F₁F₂, trục Oy là đường trung trực của F₁F₂ và F₂ nằm trên tia Ox (Hình 52). Khi đó, F₁(– c; 0) và F₂(c; 0) là hai tiêu điểm của elip (E). Chứng minh rằng:

a) A₁(– a; 0) và A₂(a; 0) đều là giao điểm của elip (E) với trục Ox.

b) B₁(0; – b) và B₂(0; b), ở đó $b = \sqrt{a^{2} - c^{2}}$ , đều là giao điểm của elip (E) với trục Oy.

Trong mặt phẳng, xét đường elip (E) là tập hợp các điểm M

Lời giải:

Trong mặt phẳng, xét đường elip (E) là tập hợp các điểm M

Do đó: A₁F₁ + A₂F₂ = a – c + a + c = 2a.

Vậy điểm A₁(– a; 0) thuộc elip (E).

Mà A₁(– a; 0) thuộc trục Ox nên A₁(– a; 0) là giao điểm của elip (E) với trục Ox.

Tương tự, ta chứng minh được A₂(a; 0) là giao điểm của elip (E) với trục Ox.

b) Vì $b = \sqrt{a^{2} - c^{2}}$ nên $b^{2} = a^{2} - c^{2} \Leftrightarrow a^{2} = b^{2} + c^{2}$ .

Ta có: $B_{2} F_{1} = \sqrt{{(- c - 0)}^{2} + {(0 - b)}^{2}} = \sqrt{c^{2} + b^{2}} = \sqrt{a^{2}} = a$ (do a > 0).

$B_{2} F_{2} = \sqrt{{(c - 0)}^{2} + {(0 - b)}^{2}} = \sqrt{c^{2} + b^{2}} = \sqrt{a^{2}} = a$ (do a > 0).

Do đó B₂F₁ = B₂F₂ = a nên B₂F₁ + B₂F₂ = a + a = 2a. Do đó, B₂(0; b) thuộc elip (E).

Mà B₂(0; b) thuộc trung Oy nên B₂(0; b) là giao điểm của elip (E) với trục Oy.

Tương tự, ta chứng minh được B₁(0; – b) là giao điểm của elip (E) với trục Oy.

Lời giải Toán 10 Bài 6: Ba đường conic hay, chi tiết khác:

Xem thêm lời giải bài tập Toán lớp 10 Cánh diều hay, chi tiết khác:

❮ Bài trước Bài sau ❯

Giải Toán lớp 10 Cánh diều

Hoạt động 2 trang 94 Toán lớp 10 Tập 2 Cánh diều

Giải Toán lớp 10 Bài 6: Ba đường conic

Xem thêm lời giải bài tập Toán lớp 10 Cánh diều hay, chi tiết khác: