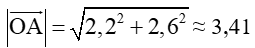Bài 6 trang 63 Toán lớp 10 Tập 2 Chân trời sáng tạo | Giải Toán 10
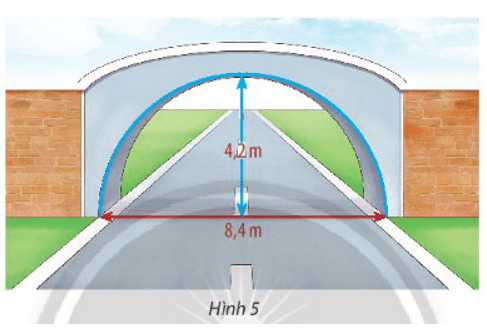
Một cái cổng hình bán nguyệt rộng 8,4m, cao 4,2 m như Hình 5. Mặt đường dưới cổng được chia thành hai làn cho xe ra vào.
Giải Toán lớp 10 Bài 3: Đường tròn trong mặt phẳng toạ độ
Bài 6 trang 63 Toán lớp 10 Tập 2: Một cái cổng hình bán nguyệt rộng 8,4m, cao 4,2 m như Hình 5. Mặt đường dưới cổng được chia thành hai làn cho xe ra vào.
a) Viết phương trình mô phỏng cái cổng.
b) Một chiếc xe tải rộng 2,2m và cao 2,6m đi đúng làn đường quy định có thể đi qua cổng mà không làm hư hỏng cổng hay không?
Lời giải:
a) Đặt hệ trục tọa độ như hình vẽ:
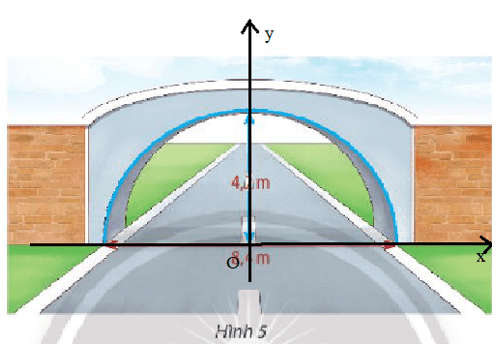
Cổng hình bán nguyệt nghĩa là một nửa đường tròn:
Tâm của đường tròn là gốc O(0; 0).
Bán kính của đường tròn là R = 4,2.
Khi đó phương trình đường tròn (phương trình mô phỏng cổng với y ≥ 0) là:
(x – 0)2 + (y – 0)2 = 4,22
⇔ x2 + y2 = 17,76
Vậy phương trình mô phỏng cổng là x2 + y2 = 17,76 (với y ≥ 0).
b) Gọi điểm cao nhất của chiếc xe tải là A, tọa độ điểm A(2,2; 2,6). Để biết được xe tải đi đúng làn đường quy định mà có thể đi qua cổng mà không làm hư hỏng cổng hay không nghĩa là điểm A phải nằm trong đường tròn hay nói cách khác là khoảng cách từ A đến tâm của đường tròn nhỏ hơn bán kính.
Ta có: = (2,2; 2,6) ⇒
Vì 3,41 < 4,2 nên điểm A nằm trong đường tròn đã cho.
Vậy một chiếc xe tải rộng 2,2m và cao 2,6m đi đúng làn đường quy định có thể đi qua cổng mà không làm hư hỏng cổng.
Lời giải bài tập Toán 10 Bài 3: Đường tròn trong mặt phẳng toạ độ hay, chi tiết khác: