Cho tam giác ABC. Gọi M là trung điểm BC và N là trung điểm AM. Đường thẳng
Câu hỏi:
Cho tam giác ABC. Gọi M là trung điểm BC và N là trung điểm AM. Đường thẳng BN cắt AC tại P. Khi đó thì giá trị của x là:
A.
B.
C.
D.
Trả lời:
Hướng dẫn giải
Đáp án đúng là: C
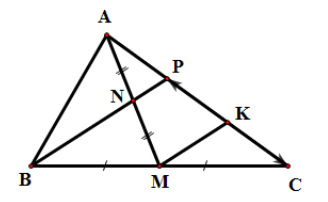
Kẻ MK // BP (K ∈ AC). Do M là trung điểm BC nên ta suy ra K là trung điểm CP (1).
Vì MK // NP, mà N là trung điểm AM nên ta suy ra P là trung điểm AK (2).
Từ (1), (2) ta suy ra AP = PK = KC.
Do đó AP = CP.
Ta có AC = AP + CP.
Suy ra AC = CP.
Vì ngược hướng với nhau.
Nên .
Do đó x = .
Vậy ta chọn đáp án C.
Xem thêm bài tập trắc nghiệm Toán 10 CTST có lời giải hay khác:
Câu 1:
Cho tam giác ABC vuông tại A có AB = 3, AC = 4. Tính độ dài .
Xem lời giải »
Câu 2:
Cho và điểm O. Gọi M, N lần lượt là hai điểm thỏa mãn và . Tìm .
Xem lời giải »
Câu 3:
Cho tam giác ABC có trọng tâm G. Gọi các điểm D, E, F lần lượt là trung điểm của các cạnh BC, CA và AB. Trong các khẳng định sau, khẳng định nào đúng?
Xem lời giải »
Câu 4:
Cho ba điểm phân biệt A, B, C. Nếu thì đẳng thức nào dưới đây đúng?
Xem lời giải »
Câu 5:
Cho tam giác OAB vuông cân tại O với OA = OB = a. Độ dài của là:
Xem lời giải »
Câu 6:
Cho tam giác ABC có trọng tâm G. Biểu diễn theo hai vectơ .
Xem lời giải »
Câu 7:
Cho tứ giác ABCD. Gọi M, N lần lượt là trung điểm AB, CD. Khi đó bằng
Xem lời giải »
Câu 8:
Cho hình bình hành ABCD tâm O và điểm M bất kỳ. Khẳng định nào sau đây đúng?
Xem lời giải »


