Tập nghiệm của bất phương trình 2x^2 – 7x – 15 > = 0 là:
Câu hỏi:
Tập nghiệm của bất phương trình 2x2 – 7x – 15 ≥ 0 là:
A.\[\left( {--\infty ; - \frac{3}{2}} \right] \cup [5; + \infty )\];
B.\(\left[ { - \frac{3}{2};5} \right]\);
C.\[\left( {--\infty ; - 5} \right] \cup \left[ {\frac{3}{2}; + \infty } \right)\];
D.\(\left[ { - 5;\frac{3}{2}} \right]\).
Trả lời:
Đáp án đúng là: A
Xét tam thức f(x) = 2x2 – 7x – 15 có ∆ = 169 > 0, hai nghiệm phân biệt là x = 5; x = \( - \frac{3}{2}\) và a = 2 > 0.
Ta có bảng xét dấu :
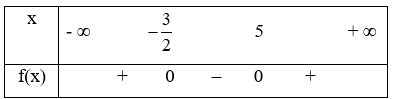
Từ bảng xét dấu ta có tập nghiệm của bất phương trình là \[\left( {--\infty ; - \frac{3}{2}}

