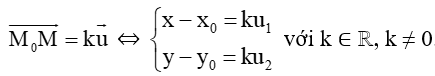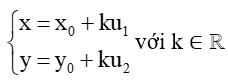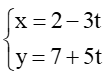Giải Toán 10 trang 47 Tập 2 Chân trời sáng tạo

Haylamdo biên soạn và sưu tầm giải Toán 10 trang 47 Tập 2 trong Bài 2: Đường thẳng trong mặt phẳng toạ độ Toán lớp 10 Tập 2 Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 10 trang 47.

Giải Toán 10 trang 47 Tập 2 Chân trời sáng tạo

Hoạt động khám phá 2 trang 47 Toán lớp 10 Tập 2: Trong mặt phẳng Oxy, cho đường thẳng ∆ đi qua điểm M₀(x₀; y₀) và nhận $\overrightarrow{u}$ = (u₁; u₂) làm VTCP. Với mỗi điểm M(x; y) thuộc ∆, tìm tọa độ điểm M theo tọa độ M₀ và $\overrightarrow{u}$.

Lời giải:

Ta có $\overrightarrow{M_{0}M}$(x – x₀; y – y₀)

Vì $\overrightarrow{u}$ là VTCP của đường thẳng ∆ nên vectơ $\overrightarrow{M_{0}M}$ và $\overrightarrow{u}$ cùng phương.

Khi đó ta có:

⇔

Vậy M(x₀ + ku₁; y₀ + ku₂).

Thực hành 1 trang 47 Toán lớp 10 Tập 2:

a) Viết phương trình tham số của đường thẳng d đi qua điểm B(-9; 5) và nhận vectơ $\overrightarrow{v}$ = (8; -4) làm vectơ chỉ phương.

b) Tìm tọa độ P trên ∆, biết P có tung độ bằng 1.

Lời giải:

a) Phương trình tham số của đường thẳng d đi qua điểm B(-9; 5) và nhận vectơ $\overrightarrow{v}$ = (8; -4) làm vectơ chỉ phương là: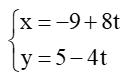

b)

Phương trình tham số của đường thẳng ∆ là

Vì P ∈ ∆ nên tọa độ điểm P là P(2 – 3t; 7 + 5t).

Ta lại có tung độ của điểm P bằng 1 nên 7 + 5t = 1

⇔ 5t = 1 – 7

⇔ 5t = -6

⇔ t = $-\frac{6}{5}$

⇒ P = $\left(2-3.\left(-\frac{6}{5}\right);7+5.\left(-\frac{6}{5}\right)\right)=\left(\frac{28}{5};1\right)$.

Vậy P$\left(\frac{28}{5};1\right)$.

Lời giải bài tập Toán lớp 10 Bài 2: Đường thẳng trong mặt phẳng toạ độ Chân trời sáng tạo hay khác:

• Giải Toán 10 trang 46 Tập 2

• Giải Toán 10 trang 48 Tập 2

• Giải Toán 10 trang 49 Tập 2

• Giải Toán 10 trang 51 Tập 2

• Giải Toán 10 trang 53 Tập 2

• Giải Toán 10 trang 54 Tập 2

• Giải Toán 10 trang 56 Tập 2

• Giải Toán 10 trang 57 Tập 2

• Giải Toán 10 trang 58 Tập 2