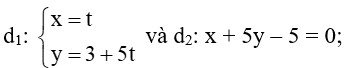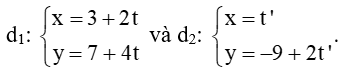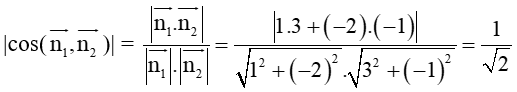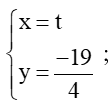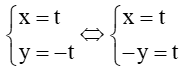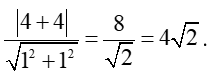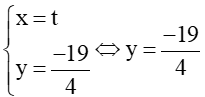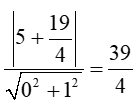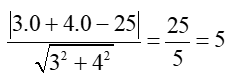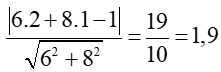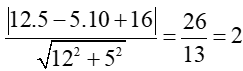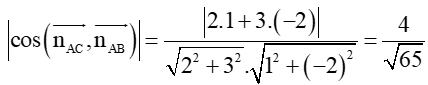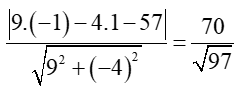Giải Toán 10 trang 58 Tập 2 Chân trời sáng tạo

❮ Bài trước Bài sau ❯

Haylamdo biên soạn và sưu tầm giải Toán 10 trang 58 Tập 2 trong Bài 2: Đường thẳng trong mặt phẳng toạ độ Toán lớp 10 Tập 2 Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 10 trang 58.

Giải Toán 10 trang 58 Tập 2 Chân trời sáng tạo

Bài 5 trang 58 Toán lớp 10 Tập 2: Cho đường thẳng d có phương trình tham số 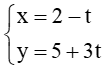. Tìm giao điểm của d với hai trục tọa độ.

Lời giải:

+) Gọi A là giao điểm của đường thẳng d với trục Ox.

Vì A thuộc đường thẳng d nên tọa độ điểm A(2 – t; 5 + 3t).

Mặt khác A cũng thuộc trục Ox nên tung độ của A bằng 0 hay 5 + 3t = 0 ⇔ t = $- \frac{5}{3}$ .

⇒2 – t = $2 - (- \frac{5}{3}) = \frac{11}{3}$ .

Do đó $A (\frac{11}{3}; 0)$ .

+) Gọi B là giao điểm của đường thẳng d với trục Oy.

Vì B thuộc đường thẳng d nên tọa độ điểm B(2 – t; 5 + 3t).

Mặt khác B cũng thuộc trục Oy nên hoành độ của B bằng 0 hay 2 – t = 0 ⇔ t = 2.

⇒ 5 + 3t = 5 + 3.2 = 5 + 6 = 11

Do đó B(0; 11).

Vậy tọa độ giao điểm của đường thẳng d với hai trục Ox và Oy lần lượt là $A (\frac{11}{3}; 0)$ và B(0; 11).

Bài 6 trang 58 Toán lớp 10 Tập 2: Tìm số đo của góc giữa hai đường thẳng d₁ và d₂ trong các trường hợp:

a) d₁: x – 2y + 3 = 0 và d₂: 3x – y – 11 = 0;

b) Tìm số đo của góc giữa hai đường thẳng d1 và d2 trong các trường hợp

c) Tìm số đo của góc giữa hai đường thẳng d1 và d2 trong các trường hợp

Lời giải:

a) Ta có:

VTPT của đường thẳng d₁: x – 2y + 3 = 0 là $\vec{n_{1}}$ (1; -2).

VTPT của đường thẳng d₂: 3x – y – 11 = 0 là $\vec{n_{2}}$ (3; -1).

Áp dụng công thức tính góc giữa hai đường thẳng ta có:

cos(d₁; d₂) = Tìm số đo của góc giữa hai đường thẳng d1 và d2 trong các trường hợp

⇒ (d₁; d₂) = 45°.

Vậy góc giữa hai đường thẳng d₁ và d₂ là 45°.

b) Ta có :

VTCP của đường thẳng d₁: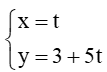 Tìm số đo của góc giữa hai đường thẳng d1 và d2 trong các trường hợp là $\vec{u_{1}}$ (1; 5) hay VTPT là $\vec{n_{1}}$ (5; -1)

VTPT của đường thẳng d₂ : x + 5y – 5 = 0 là $\vec{n_{2}}$ (1; 5).

Ta nhận thấy $\vec{n_{1}} . \vec{n_{2}}$ = 5.1 + (-1).5 = 5 – 5 = 0. Do đó $\vec{n_{1}}$ ⊥ $\vec{n_{2}}$ hay hai đường thẳng d₁ và d₂ vuông góc.

Vậy góc giữa hai đường thẳng d₁ và d₂ là 90°.

c) Ta có:

VTCP của đường thẳng d₁ :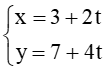 Tìm số đo của góc giữa hai đường thẳng d1 và d2 trong các trường hợp là $\vec{u_{1}}$ (2; 4);

VTCP của đường thẳng d₂ :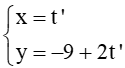 Tìm số đo của góc giữa hai đường thẳng d1 và d2 trong các trường hợp là $\vec{u_{2}}$ (1; 2).

Ta nhận thấy $\vec{u_{1}}$ = (2; 4) = 2(1; 2) = 2 $\vec{u_{2}}$ nên $\vec{u_{1}}$ và $\vec{u_{2}}$ cùng phương. Do đó d₁ song song hoặc trùng d₂.

Vậy góc giữa hai đường thẳng d₁ và d₂ bằng 0°.

Bài 7 trang 58 Toán lớp 10 Tập 2: Tính khoảng cách từ điểm M đến đường thẳng ∆ trong các trường hợp sau:

a) M(1; 2) và ∆: 3x – 4y + 12 = 0;

b) M(4; 4) và ∆: Tính khoảng cách từ điểm M đến đường thẳng ∆ trong các trường hợp sau

c) M(0; 5) và ∆: Tính khoảng cách từ điểm M đến đường thẳng ∆ trong các trường hợp sau

d) M(0; 0) và ∆: 3x + 4y – 25 = 0.

Lời giải:

a) Áp dụng công thức tính khoảng cách từ một điểm đến đường thẳng ta được:

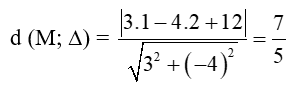
Vậy khoảng cách từ điểm M đến đường thẳng ∆ là $\frac{7}{5}$ .

b) Xét đường thẳng ∆: Tính khoảng cách từ điểm M đến đường thẳng ∆ trong các trường hợp sau

⇒ x = - y

⇔ x + y = 0

Áp dụng công thức tính khoảng cách từ một điểm đến đường thẳng ta được:

d(M; ∆) = Tính khoảng cách từ điểm M đến đường thẳng ∆ trong các trường hợp sau

Vậy khoảng cách từ điểm M đến đường thẳng ∆ là $4 \sqrt{2}$ .

c) Xét đường thẳng ∆: Tính khoảng cách từ điểm M đến đường thẳng ∆ trong các trường hợp sau

⇔ y + $\frac{19}{4}$ = 0

Áp dụng công thức tính khoảng cách từ một điểm đến đường thẳng ta được:

d(M; ∆) = Tính khoảng cách từ điểm M đến đường thẳng ∆ trong các trường hợp sau

Vậy khoảng cách từ điểm M đến đường thẳng ∆ là $\frac{39}{4}$ .

d) Áp dụng công thức tính khoảng cách từ một điểm đến đường thẳng ta được:

d(M; ∆) = Tính khoảng cách từ điểm M đến đường thẳng ∆ trong các trường hợp sau

Vậy khoảng cách từ điểm M đến đường thẳng ∆ là 5.

Bài 8 trang 58 Toán lớp 10 Tập 2: Tính khoảng cách giữa hai đường thẳng ∆: 3x + 4y – 10 = 0 và ∆’: 6x + 8y – 1 = 0.

Lời giải:

Đường thẳng ∆: 3x + 4y – 10 = 0 có VTPT là $\vec{n_{1}}$ (3; 4);

Đường thẳng ∆’: 6x + 8y – 1 = 0 có VTPT là $\vec{n_{2}}$ (6; 8).

Ta có $\vec{n_{2}}$ = 2 $\vec{n_{1}}$ nên hai vec tơ $\vec{n_{1}}$ và $\vec{n_{2}}$ cùng phương. Suy ra hai đường thẳng ∆ và ∆’ song song hoặc trùng nhau.

Lấy M(2; 1) thuộc đường thẳng ∆.

Áp dụng công thức tính khoảng cách từ một điểm đến đường thẳng ta được:

d(M; ∆’) = Tính khoảng cách giữa hai đường thẳng ∆: 3x + 4y – 10 = 0 và ∆’: 6x + 8y – 1 = 0

Vậy khoảng cách giữa hai đường thẳng ∆ và ∆’ là 1,9.

Bài 9 trang 58 Toán lớp 10 Tập 2: Trong mặt phẳng Oxy, cho điểm S(x; y) di động trên đường thẳng d: 12x – 5y + 16 = 0. Tính khoảng cách ngắn nhất từ điểm M(5; 10) đển điểm S.

Lời giải:

Khoảng cách ngắn nhất từ điểm M đến điểm S khi MS vuông góc với đường thẳng d hay chính là khoảng cách từ điểm M đến đường thẳng d.

Áp dụng công thức tính khoảng cách từ một điểm đến đường thẳng ta có:

MS = d(M; d) = Trong mặt phẳng Oxy, cho điểm S(x; y) di động trên đường thẳng d: 12x – 5y + 16 = 0

Vậy khoảng cách ngắn nhất từ điểm M(5; 10) đển điểm S là bằng 2.

Bài 10 trang 58 Toán lớp 10 Tập 2: Một người đang viết chương trình cho trò chơi bóng đá rô bốt. Gọi A(-1; 1), B(9; 6), C(5; -3) là ba vị trí trên màn hình.

a) Viết phương trình các đường thẳng AB, AC, BC.

b) Tính góc hợp bởi hai đường thẳng AB và AC.

c) Tính khoảng cách từ điểm A đến đường thẳng BC.

Lời giải:

+) Ta có $\vec{A B}$ = (10; 5) là VTCP của đường thẳng AB. Do đó VTPT của đường thẳng AB AB là $\vec{n_{A B}}$ (1; -2).

Phương trình đường thẳng AB đi qua điểm A(-1; 1) và nhận $\vec{n_{A B}}$ (1; -2) làm VTPT, ta được:

(x + 1) – 2(y – 1) = 0

⇔ x – 2y + 3 = 0.

Vậy phương trình đường thẳng AB là x – 2y + 3 = 0.

+) Ta có $\vec{A C}$ = (6; -4) là VTCP của đường thẳng AC. Do đó VTPT của đường thẳng AC là $\vec{n_{A C}}$ (2; 3).

Phương trình đường thẳng AC đi qua điểm A(-1; 1) và nhận $\vec{n_{A C}}$ (2; 3) làm VTPT, ta được:

2(x + 1) + 3(y – 1) = 0

⇔ 2x + 3y – 1 = 0.

Vậy phương trình đường thẳng AC là 2x + 3y – 1 = 0.

+) Ta có $\vec{B C}$ = (-4; -9) là VTCP của đường thẳng BC. Do đó VTPT của đường thẳng BC là $\vec{n_{B C}}$ (9; -4).

Phương trình đường thẳng BC đi qua điểm B(9; 6) và nhận $\vec{n_{B C}}$ (9; -4) làm VTPT, ta được:

9(x – 9) – 4(y – 6) = 0

⇔ 9x – 4y – 57 = 0.

Vậy phương trình đường thẳng BC là 9x – 4y – 57 = 0.

b) Áp dụng công thức tính góc giữa hai đường thẳng ta có:

cos(AB; AC) = Một người đang viết chương trình cho trò chơi bóng đá rô bốt

⇒ (AB; AC) = 60,26°.

Vậy góc giữa hai đường thẳng AB và AC là 60,26°.

c) Áp dụng công thức tính khoảng cách từ một điểm đến đường thẳng, ta có:

d(A; BC) = Một người đang viết chương trình cho trò chơi bóng đá rô bốt

Vậy khoảng cách từ điểm A đến đường thẳng BC là $\frac{70}{\sqrt{97}}$ .

Lời giải bài tập Toán lớp 10 Bài 2: Đường thẳng trong mặt phẳng toạ độ Chân trời sáng tạo hay khác:

Xem thêm lời giải bài tập Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:

❮ Bài trước Bài sau ❯