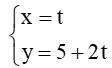Giải Toán 10 trang 51 Tập 2 Chân trời sáng tạo

---

Haylamdo biên soạn và sưu tầm giải Toán 10 trang 51 Tập 2 trong Bài 2: Đường thẳng trong mặt phẳng toạ độ Toán lớp 10 Tập 2 Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 10 trang 51.

Giải Toán 10 trang 51 Tập 2 Chân trời sáng tạo

Thực hành 3 trang 51 Toán lớp 10 Tập 2: Tìm các hàm số bậc nhất có đồ thị là các đường thẳng trong thực hành 2.

Lời giải:

a) Phương trình tổng quát của đường thẳng ∆ đi qua điểm A(1; 1) và có vectơ pháp tuyến $\overrightarrow{n}$ = (3; 5) là 3x + 5y – 8 = 0.

Khi đó ta có thể viết:

3x + 5y – 8 = 0

⇔ 5y = – 3x + 8

⇔ y = $-\frac{3}{5}$x + $\frac{8}{5}$

Vậy đường thẳng ∆ đã cho là đồ thị của hàm bậc nhất y = $-\frac{3}{5}$x + $\frac{8}{5}$ có hệ số góc k = $-\frac{3}{5}$.

b) Phương trình tổng quát của đường thẳng ∆ đi qua điểm O(0; 0) và có vectơ pháp tuyến $\overrightarrow{n}$ = (7; 2) là: 7x + 2y = 0.

Khi đó ta có thể viết:

7x + 2y = 0

⇔ 2y = –7x

⇔ y = $-\frac{7}{2}$x

Vậy đường thẳng ∆ đã cho là đồ thị của hàm số bậc nhất y = $-\frac{7}{2}$x với hệ số góc k = $-\frac{7}{2}$.

c) Khi đó phương trình tổng quát của đường thẳng ∆ đi qua điểm M(4; 0) và có vectơ pháp tuyến $\overrightarrow{n}$ = (3; 4) là: 3x + 4y – 12 = 0.

Khi đó ta có thể viết:

3x + 4y – 12 = 0

⇔ 4y = –3x + 12

⇔ y = $-\frac{3}{4}$x + 3

Vậy đường thẳng ∆ là đồ thị của hàm bậc nhất y = $-\frac{3}{4}$x + 3 có hệ số góc k = $-\frac{3}{4}$.

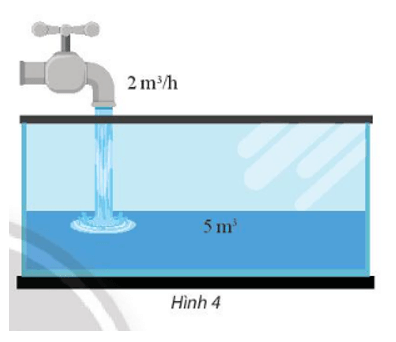
Vận dụng 3 trang 51 Toán lớp 10 Tập 2: Một người bắt đầu mở một vòi nước. Nước từ vòi chảy với tốc độ là 2m³/h vào một cái bể đã chứa sẵn 5m³ nước.

a) Viết biểu thức tính thể tích y của nước có trong bể sau x giờ.

b) Gọi y = f(x) là hàm số xác định được từ câu a). Vẽ đồ thị d của hàm số này.

c) Viết phương trình tham số và phương trình tổng quát của đường thẳng d.

Lời giải:

a) Sau x giờ, lượng nước chảy vào bể là: 2x (m³).

Vì trong bể có sẵn 5m³ nước nên sau x giờ thể tích nước y có trong bể là: y = 5 + 2x (m³).

Vậy biểu thức tính thể tích y của nước có trong bể sau x giờ là: y = 2x + 5.

b) Ta có: y = f(x) = 2x + 5.

Chọn x = 0 ⇒ y = 5. Ta có điểm A(0; 5).

Chọn x = -1 ⇒ y = 3. Ta có điểm B(-1; 3).

Đồ thị d của hàm số là đường thẳng đi qua hai điểm A và B. Ta có hình vẽ:

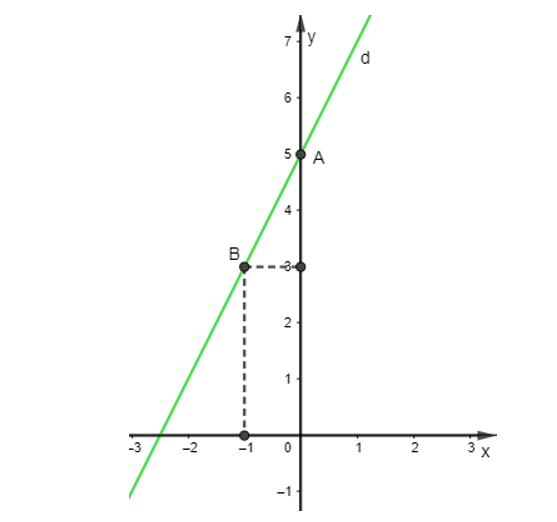
c) Ta có đồ thị hàm số bậc nhất của đường thẳng d là: y = 2x + 5

⇔ - 2x + y – 5 = 0

Suy ra phương trình tổng quát của đường thẳng d là: - 2x + y – 5 = 0.

Từ phương trình tổng quát ta có vectơ pháp tuyến của d là $\overrightarrow{n}$(-2; 1). Do đó vectơ chỉ phương của đường thẳng d là $\overrightarrow{u}$(1; 2).

Phương trình tham số của đường thẳng d đi qua điểm A(0; 5) nhận $\overrightarrow{u}$(1; 2) làm VTCP là:

Vậy phương trình tổng quát và phương trình tham số lần lượt là - 2x + y – 5 = 0 và

Hoạt động khám phá 4 trang 51 Toán lớp 10 Tập 2: Cho hai đường thẳng ∆₁ và ∆₂ có vec tơ pháp tuyến lần lượt là $\overrightarrow{n_1}$ và $\overrightarrow{n_2}$.

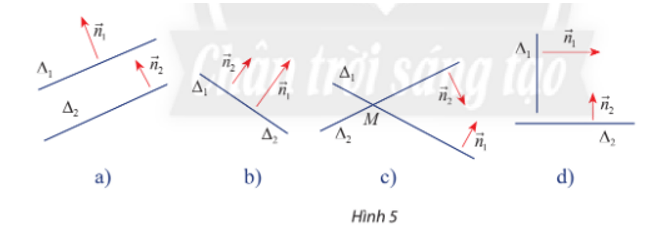
Nêu nhận xét về vị trí tương đối giữa ∆₁ và ∆₂ trong các trường hợp sau:

a) $\overrightarrow{n_1}$ và $\overrightarrow{n_2}$ cùng phương (Hình 5a, b);

b) $\overrightarrow{n_1}$ và $\overrightarrow{n_2}$ không cùng phương (Hình 5c, d);

c) $\overrightarrow{n_1}$ và $\overrightarrow{n_2}$ vuông góc (Hình 5d).

Lời giải:

a) Ta có $\overrightarrow{n_1}$ và $\overrightarrow{n_2}$ cùng phương nên $\overrightarrow{n_1}$ và $\overrightarrow{n_2}$ có giá song song hoặc trùng nhau.

Mà $\overrightarrow{n_1}$ ⊥ ∆₁ và $\overrightarrow{n_2}$ ⊥ ∆₂ nên ∆₁ // ∆₂ hoặc ∆₁ trùng ∆₂.

Vậy ∆₁ // ∆₂ hoặc ∆₁ trùng ∆₂.

b) Ta có $\overrightarrow{n_1}$ và $\overrightarrow{n_2}$ không cùng phương suy ra $\overrightarrow{n_1}$ và $\overrightarrow{n_2}$ cắt nhau nên ∆₁ và ∆₂ cắt nhau.

c) Ta có $\overrightarrow{n_1}$ và $\overrightarrow{n_2}$ vuông góc với nhau

Mà $\overrightarrow{n_1}$ ⊥ ∆₁ và $\overrightarrow{n_2}$ ⊥ ∆₂ nên ∆₁ vuông góc với ∆₂..

Lời giải bài tập Toán lớp 10 Bài 2: Đường thẳng trong mặt phẳng toạ độ Chân trời sáng tạo hay khác:

• Giải Toán 10 trang 46 Tập 2

• Giải Toán 10 trang 47 Tập 2

• Giải Toán 10 trang 48 Tập 2

• Giải Toán 10 trang 49 Tập 2

• Giải Toán 10 trang 53 Tập 2

• Giải Toán 10 trang 54 Tập 2

• Giải Toán 10 trang 56 Tập 2

• Giải Toán 10 trang 57 Tập 2

• Giải Toán 10 trang 58 Tập 2