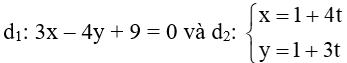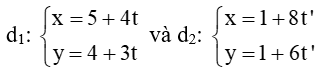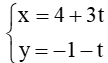Giải Toán 10 trang 53 Tập 2 Chân trời sáng tạo

---

Haylamdo biên soạn và sưu tầm giải Toán 10 trang 53 Tập 2 trong Bài 2: Đường thẳng trong mặt phẳng toạ độ Toán lớp 10 Tập 2 Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 10 trang 53.

Giải Toán 10 trang 53 Tập 2 Chân trời sáng tạo

Thực hành 4 trang 53 Toán lớp 10 Tập 2: Xét vị trí tương đối của các cặp đường thẳng d₁ và d₂ trong các trường hợp sau:

a) d₁: x – 5y + 9 = 0 và d₂: 10x + 2y + 7 = 10;

b)

c)

Lời giải:

a) Ta có d₁ và d₂ có vectơ pháp tuyến lần lượt là $\overrightarrow{n_1}$(1; -5) và $\overrightarrow{n_2}$(10; 2)

Ta lại có: $\overrightarrow{n_1}.\overrightarrow{n_2}$ = a₁a₂ – b₁b₂ = 1.10 + 2.(-5) = 0, suy ra $\overrightarrow{n_1}$ ⊥ $\overrightarrow{n_2}$ .

Do đó d₁ và d₂ là hai đường thẳng vuông góc với nhau.

b) Vec tơ chỉ phương của d₂ là $\overrightarrow{u_2}$(4;3)

Khi đó vectơ pháp tuyến của đường thẳng d₂ là $\overrightarrow{n_2}$(-3; 4).

Vectơ pháp tuyến của đường thẳng d₁ là $\overrightarrow{n_1}$(3; -4).

Ta có: a₁b₂ – b₁a₂ = (-3).(-4) – 3.4 = 0. Suy ra hai vectơ $\overrightarrow{n_1}$ và $\overrightarrow{n_2}$ cùng phương.

Do đó hai đường thẳng d₁ và d₂ song song hoặc trùng nhau.

Lấy điểm M(1; 1) thuộc đường thẳng d₂, thay tọa độ của M vào phương trình đường thẳng d₁ ta được: 3.1 – 4.1 + 9 = 8 ≠ 0, suy ra M không thuộc d₁.

Vậy hai đường thẳng d₁ và d₂ song song.

c) Đường thẳng d₁ và d₂ lần lượt có vec tơ chỉ phương là $\overrightarrow{u_1}$(4; 3) và $\overrightarrow{u_2}$(8; 6).

Ta có: a₁b₂ – b₁a₂ = 4.6 – 3.8 = 24 – 24 = 0. Suy ra hai vectơ $\overrightarrow{u_1}$ và $\overrightarrow{u_2}$ cùng phương.

Do đó hai đường thẳng d₁ và d₂ song song hoặc trùng nhau.

Lấy điểm M(1; 1) thuộc đường thẳng d₂, thay tọa độ của M vào phương trình đường thẳng d₁ ta được: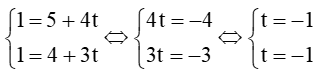, suy ra M thuộc d₁.

Vậy hai đường thẳng d₁ và d₂ trùng nhau.

Vận dụng 4 trang 53 Toán lớp 10 Tập 2: Viết phương trình đường thẳng d₁:

a) Đi qua điểm A(2; 3) và song song với đường thẳng d₂: x + 3y + 2 = 0;

b) Đi qua điểm B(4; -1) và vuông góc với đường thẳng d₃: 3x – y + 1 = 0.

Lời giải:

a) Vectơ pháp tuyến của đường thẳng d₂ là $\overrightarrow{n_2}$(1; 3).

Vì đường thẳng d₁ song song với đường thẳng d₂ nên vectơ pháp tuyến của d₂ cũng là vectơ pháp tuyến của d₁. Khi đó phương trình đường thẳng d₁ đi qua điểm A(2; 3) và nhận $\overrightarrow{n_2}$(1; 3) làm vectơ pháp tuyến là: 1(x – 2) + 3(y – 3) = 0 ⇔ x + 3y – 11 = 0.

Vậy phương trình đường thẳng d₁ là: x + 3y – 11 = 0.

b) Vectơ pháp tuyến của đường thẳng d₃ là $\overrightarrow{n_3}$(3; -1).

Vì đường thẳng d₁ vuông góc với đường thẳng d₃ nên vectơ pháp tuyến của d₃ là vectơ chỉ phương của d₁. Khi đó phương trình đường thẳng d₁ đi qua điểm B(4; -1) và nhận $\overrightarrow{n_3}$(3; -1) làm vectơ chỉ phương là: .

Vậy phương trình đường thẳng d₁ là:

Lời giải bài tập Toán lớp 10 Bài 2: Đường thẳng trong mặt phẳng toạ độ Chân trời sáng tạo hay khác:

• Giải Toán 10 trang 46 Tập 2

• Giải Toán 10 trang 47 Tập 2

• Giải Toán 10 trang 48 Tập 2

• Giải Toán 10 trang 49 Tập 2

• Giải Toán 10 trang 51 Tập 2

• Giải Toán 10 trang 54 Tập 2

• Giải Toán 10 trang 56 Tập 2

• Giải Toán 10 trang 57 Tập 2

• Giải Toán 10 trang 58 Tập 2