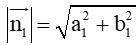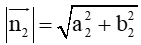Giải Toán 10 trang 54 Tập 2 Chân trời sáng tạo

❮ Bài trước Bài sau ❯

Haylamdo biên soạn và sưu tầm giải Toán 10 trang 54 Tập 2 trong Bài 2: Đường thẳng trong mặt phẳng toạ độ Toán lớp 10 Tập 2 Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 10 trang 54.

Giải Toán 10 trang 54 Tập 2 Chân trời sáng tạo

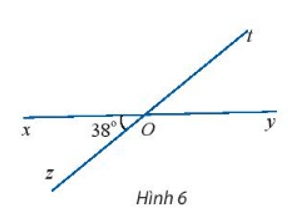
Hoạt động khám phá 5 trang 54 Toán lớp 10 Tập 2: Cho hai đường thẳng xy và zt cắt nhau tại O và cho biết $\hat{x O z} = 38 °$ (Hình 6). Tính số đo các góc $\hat{x O t}, \hat{t O y}$ và $\hat{y O z}$ .

Lời giải:

Ta có: $\hat{x O t} + \hat{x O z} = \hat{t O z}$ (hai góc kề bù)

⇔ $\hat{x O t} + 38 ° = 180 °$

⇔ $\hat{x O t} = 180 ° - 38 °$

⇔ $\hat{x O t} = 142 ° .$

Ta có hai góc $\hat{x O z}$ và $\hat{t O y}$ là hai góc đối đỉnh nên ta có $\hat{x O z} = \hat{t O y} = 38 °$ .

Ta lại có hai góc $\hat{x O t}$ và $\hat{y O z}$ là hai góc đối đỉnh nên ta có $\hat{x O t} = \hat{y O z} = 142 °$ .

Vậy $\hat{x O t} = \hat{y O z} = 142 °$ và $\hat{t O y} = 38 °$ .

Hoạt động khám phá 6 trang 54 Toán lớp 10 Tập 2: Cho hai đường thẳng: ∆₁: a₁x + b₁y + c₁ = 0 $(a_{1}^{2} + b_{1}^{2} > 0)$ > và ∆₂: a₂x + b₂y + c₂ = 0 $(a_{2}^{2} + b_{2}^{2} > 0)$ có vectơ pháp tuyến lần lượt là $\vec{n_{1}}$ và $\vec{n_{2}}$ . Tìm tọa độ của $\vec{n_{1}}$ và $\vec{n_{2}}$ và tính cos $(\vec{n_{1}}, \vec{n_{2}})$ .

Lời giải:

Đường thẳng ∆₁: a₁x + b₁y + c₁ = 0 có vectơ pháp tuyến là $\vec{n_{1}}$ (a₁; b₁) ⇒ Cho hai đường thẳng: ∆1: a1x + b1y + c1 = 0 (a1^2 + a2^2 > 0) và ∆2: a2x + b2y + c2 = 0

Đường thẳng ∆₂: a₂x + b₂y + c₂ = 0 có vectơ pháp tuyến là $\vec{n_{2}}$ (a₂; b₂) ⇒ Cho hai đường thẳng: ∆1: a1x + b1y + c1 = 0 (a1^2 + a2^2 > 0) và ∆2: a2x + b2y + c2 = 0

Ta có: $\vec{n_{1}} . \vec{n_{2}}$ = a₁.a₂ + b₁.b₂

Khi đó cos $(\vec{n_{1}}, \vec{n_{2}})$ = $\frac{a_{1} a_{2} + b_{1} . b_{2}}{\sqrt{a_{1}^{2} + b_{1}^{2}} . \sqrt{a_{2}^{2} + b_{2}^{2}}}$ .

Lời giải bài tập Toán lớp 10 Bài 2: Đường thẳng trong mặt phẳng toạ độ Chân trời sáng tạo hay khác:

Xem thêm lời giải bài tập Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:

❮ Bài trước Bài sau ❯