Giải Toán 10 trang 72 Tập 1 Chân trời sáng tạo

---

Haylamdo biên soạn và sưu tầm giải Toán 10 trang 72 Tập 1 trong Bài 2: Định lí côsin và định lí sin Toán lớp 10 Tập 1 Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 10 trang 72.

Giải Toán 10 trang 72 Tập 1 Chân trời sáng tạo

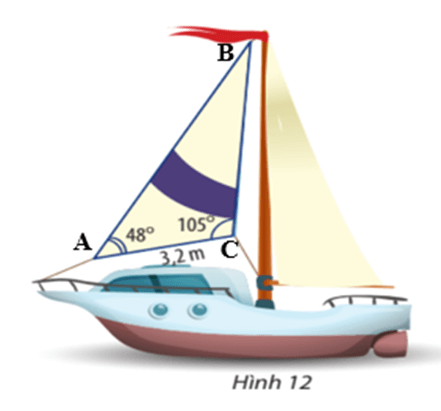
Vận dụng 3 trang 72 Toán lớp 10 Tập 1: Tính diện tích một cánh buồm hình tam giác. Biết cánh buồm đó có chiều dài một cạnh là 3,2 m và hai góc kề cạnh đó có số đo là 48° và 105° (Hình 12).

Lời giải:

Đặt tên cho các đỉnh của tam giác tạo bởi cánh buồm như hình vẽ :

Tam giác ABC có : $\widehat{A}+\widehat{B}+\widehat{C}={180}^o\Rightarrow \widehat{B}={180}^o-(\widehat{A}+\widehat{C})={180}^o-({48}^o+{105}^o)={27}^o$

Áp dụng định lí sin, ta có : $\frac{BC}{\sin A}=\frac{AC}{\sin B}=\frac{AB}{\sin C}\Rightarrow \frac{BC}{\sin {48}^o}=\frac{3,2}{\sin {27}^o}=\frac{AB}{\sin {105}^o}$

Từ $\frac{BC}{\sin {48}^o}=\frac{3,2}{\sin {27}^o}\Rightarrow BC=\frac{3,2\sin {48}^o}{\sin {27}^o}\approx 5,2$ (m).

Từ  $\frac{AB}{\sin {105}^o}=\frac{3,2}{\sin {27}^o}\Rightarrow AB=\frac{3,2\sin {105}^o}{\sin {27}^o}\approx 6,8$ (m).

Nửa chu vi của tam giác ABC là :  $p=\frac{AB+AC+BC}{2}=\frac{6,8+3,2+5,2}{2}=7,6$ (m).

Áp dụng công thức Heron ta có diện tích tam giác ABC là :

$S=\sqrt{7,6.(7,6-6,8)(7,6-3,2)(7,6-5,2)}\approx 8$

Vậy diện tích cánh buồm khoảng 8 (m²).

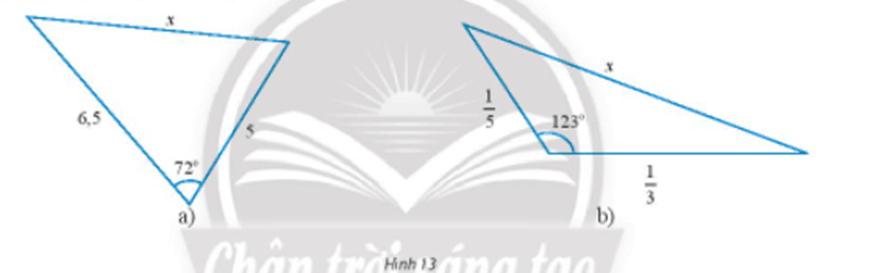
Bài 1 trang 72 Toán lớp 10 Tập 1: Tính độ dài cạnh x trong các tam giác sau :

Lời giải:

a) Áp dụng định lí côsin ta có :

x² = 6,5² + 5² – 2.6,5.5.cos72° ≈ 47,2

⇒ x = $\sqrt{47,2}$ ≈ 6,9.

Vậy x ≈ 6,9.

b) ) Áp dụng định lí côsin ta có :

$x^2={\left(\frac{1}{3}\right)}^2+{\left(\frac{1}{5}\right)}^2-2.\frac{1}{3}.\frac{1}{5}.\cos {123}^o\approx 0,22$

⇒ x = $\sqrt{0,22}$ ≈ 0,47.

Vậy x ≈ 0,47.

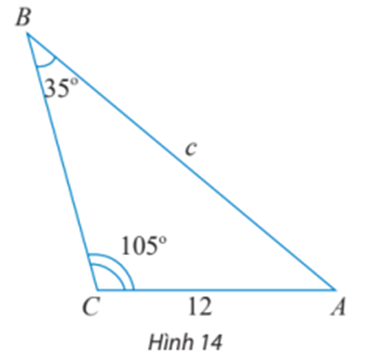
Bài 2 trang 72 Toán lớp 10 Tập 1: Tính độ dài cạnh c trong tam giác ABC ở Hình 14.

Lời giải:

Áp dụng định lí sin cho tam giác ABC ta có :

$\frac{AB}{\sin C}=\frac{AC}{\sin B}\Rightarrow \frac{c}{\sin {105}^o}=\frac{12}{\sin {35}^o}\Rightarrow c=\frac{12\sin {105}^o}{\sin {35}^o}\approx 20,21$

Vậy c ≈ 20,21.

Bài 3 trang 72 Toán lớp 10 Tập 1: Cho tam giác ABC, biết cạnh a = 152, $\widehat{B}={79}^o,\widehat{C}={61}^o$. Tính các góc, các cạnh còn lại và bán kính đường tròn ngoại tiếp của tam giác đó.

Lời giải:

Tam giác ABC có $\widehat{A}+\widehat{B}+\widehat{C}={180}^o\Rightarrow \widehat{A}={180}^o-(\widehat{B}+\widehat{C})={180}^o-({79}^o+{61}^o)={40}^o$.

Áp dụng định lí sin ta có: $\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}=2R\Rightarrow \frac{152}{\sin {40}^o}=\frac{b}{\sin {79}^o}=\frac{c}{\sin {61}^o}=2R$ .

Từ $\frac{152}{\sin {40}^o}=\frac{b}{\sin {79}^o}\Rightarrow b=\frac{152\sin {79}^o}{\sin {40}^o}\approx 232,13$

Từ $\frac{152}{\sin {40}^o}=\frac{c}{\sin {61}^o}\Rightarrow c=\frac{152.\sin {61}^o}{\sin {40}^o}\approx 206,82$

Từ $\frac{152}{\sin {40}^o}=2R\Rightarrow R=\frac{152}{2\sin {40}^o}\approx 118,24$

Vậy góc và các cạnh còn lại, bán kính đường tròn ngoại tiếp  của tam giác ABC là:

  $\widehat{A}={40}^o$; AC = b ≈ 232,13 ; AB = c ≈ 206,82; R ≈ 118,24.

Lời giải bài tập Toán lớp 10 Bài 2: Định lí côsin và định lí sin Chân trời sáng tạo hay khác:

• Giải Toán 10 trang 65

• Giải Toán 10 trang 66

• Giải Toán 10 trang 67

• Giải Toán 10 trang 69

• Giải Toán 10 trang 70

• Giải Toán 10 trang 71

• Giải Toán 10 trang 73