Giải Toán 10 trang 73 Tập 1 Chân trời sáng tạo

---

Haylamdo biên soạn và sưu tầm giải Toán 10 trang 73 Tập 1 trong Bài 2: Định lí côsin và định lí sin Toán lớp 10 Tập 1 Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 10 trang 73.

Giải Toán 10 trang 73 Tập 1 Chân trời sáng tạo

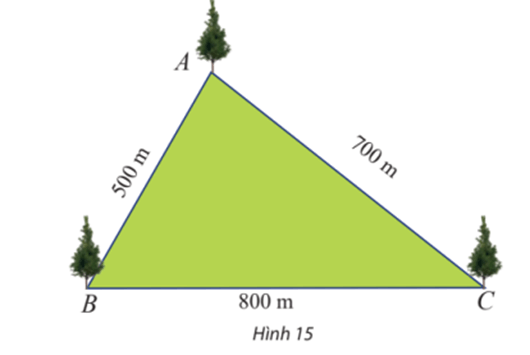
Bài 4 trang 73 Toán lớp 10 Tập 1: Một công viên có dạng hình tam giác với các kích thước như Hình 15. Tính số đo các góc của tam giác đó.

Lời giải:

Áp dụng hệ quả của định lí côsin cho tam giác ABC ta có:

$\cos A=\frac{A{B}^2+A{C}^2-B{C}^2}{2.AB.AC}=\frac{{500}^2+{700}^2-{800}^2}{\mathrm{2.500.700}}\approx 0,143$

⇒  $\widehat{A}$ ≈ 82°.

$\cos B=\frac{A{B}^2+B{C}^2-A{C}^2}{2.AB.BC}=\frac{{500}^2+{800}^2-{700}^2}{\mathrm{2.500.800}}=0,5$

⇒ $\widehat{B}$ = 60°.

Tam giác ABC có $\widehat{A}+\widehat{B}+\widehat{C}={180}^o\Rightarrow \widehat{C}={180}^o-(\widehat{A}+\widehat{B})={180}^o-({82}^o+{60}^o)={38}^o$.

Vậy các góc của tam giác ABC là:  $\widehat{A}$ ≈ 82°, $\widehat{B}$ = 60°; $\widehat{C}$ = 38°.

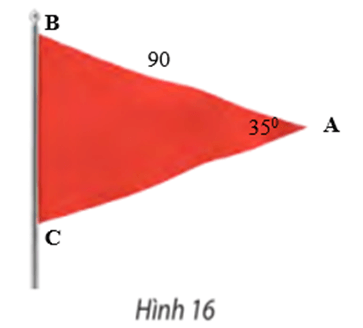
Bài 5 trang 73 Toán lớp 10 Tập 1: Tính diện tích một lá cờ hình tam giác cân có độ dài cạnh bên là 90 cm và góc ở đỉnh là 35°.

Lời giải:

Đặt tên các đỉnh của lá cờ hình tam giác như sau:

Vì tam giác ABC cân tại A nên AB = AC = 90 cm, $\widehat{A}={35}^o$

Áp dụng công thức tính diện tích ta có diện tích tam giác ABC là:

$S=\frac{1}{2}.AC.AB.\sin A=\frac{1}{2}\mathrm{.90.90.}\sin {35}^o\approx 2\text{ 323}$ (cm²).

Vậy diện tích của lá cờ khoảng  2 323 cm².

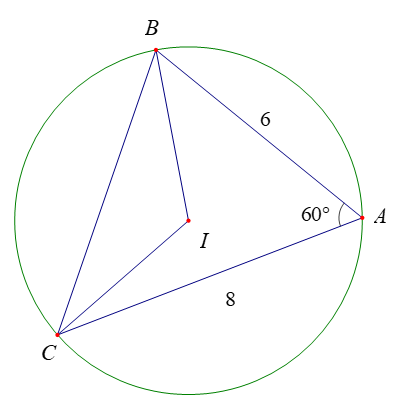
Bài 6 trang 73 Toán lớp 10 Tập 1: Cho tam giác ABC có AB = 6, AC = 8 và $\widehat{A}={60}^o$.

a) Tính diện tích tam giác ABC.

b) Gọi I là tâm đường tròn ngoại tiếp tam giác ABC. Tính diện tích tam giác IBC.

Lời giải:

a) Áp dụng công thức tính diện tích tam giác ta có:

$S=\frac{1}{2}.AC.AB.\sin A=\frac{1}{2}\mathrm{.6.8.}\sin {60}^o=\frac{1}{2}\mathrm{.6.8.}\frac{\sqrt{3}}{2}=12\sqrt{3}\approx 20,8$

Vậy diện tích tam giác ABC là 20,8 (đơn vị diện tích).

b) Áp dụng định lí côsin cho tam giác ABC ta có:

BC² = AB² + AC² – 2.AB.AC.cosA = 6² + 8² –  2.6.8.cos60° = 52

⇒ BC = $\sqrt{52}$ ≈ 7,2.

Mặt khác diện tích tam giác ABC:     

$S=\frac{AB.AC.BC}{4R}\Rightarrow R=\frac{AB.AC.BC}{4S}=\frac{\mathrm{6.8.}\sqrt{52}}{4.12\sqrt{3}}\approx 4,2$

Vì I là tâm đường tròn ngoại tiếp tam giác ABC nên ta có IA = IB = IC = R = 4,2.

Nửa chu vi của tam giác IBC: $p=\frac{IB+IC+BC}{2}=\frac{4,2+4,2+7,2}{2}=7,8$

Áp dụng công thức Heron ta tính được diện tích tam giác IBC:

$S=\sqrt{7,8.(7,8-4,2).(7,8-4,2).(7,8-7,2)}\approx \sqrt{60,7}\approx 7,8$

Vậy diện tích tam giác IBC là 7,8 (đơn vị diện tích).

a) Áp dụng công thức tính diện tích tam giác ta có:

$S=\frac{1}{2}.AC.AB.\sin A=\frac{1}{2}\mathrm{.6.8.}\sin {60}^o=\frac{1}{2}\mathrm{.6.8.}\frac{\sqrt{3}}{2}=12\sqrt{3}\approx 20,8$

Vậy diện tích tam giác ABC là 20,8 (đơn vị diện tích).

b) Áp dụng định lí côsin cho tam giác ABC ta có:

BC² = AB² + AC² – 2.AB.AC.cosA = 6² + 8² –  2.6.8.cos60° = 52

⇒ BC = $\sqrt{52}$ ≈ 7,2.

Mặt khác diện tích tam giác ABC:     

$S=\frac{AB.AC.BC}{4R}\Rightarrow R=\frac{AB.AC.BC}{4S}=\frac{\mathrm{6.8.}\sqrt{52}}{4.12\sqrt{3}}\approx 4,2$

Vì I là tâm đường tròn ngoại tiếp tam giác ABC nên ta có IA = IB = IC = R = 4,2.

Nửa chu vi của tam giác IBC: $p=\frac{IB+IC+BC}{2}=\frac{4,2+4,2+7,2}{2}=7,8$

Áp dụng công thức Heron ta tính được diện tích tam giác IBC:

$S=\sqrt{7,8.(7,8-4,2).(7,8-4,2).(7,8-7,2)}\approx \sqrt{60,7}\approx 7,8$

Vậy diện tích tam giác IBC là 7,8 (đơn vị diện tích).

Bài 7 trang 73 Toán lớp 10 Tập 1: Cho tam giác ABC có trọng tâm G và độ dài ba cạnh AB, BC, CA lần lượt là 15, 18, 27.

a) Tính diện tích và bán kính đường tròn nội tiếp tam giác ABC.

b) Tính diện tích tam giác GBC.

Lời giải:

a) Nửa chu vi của tam giác ABC là : $p=\frac{15+18+27}{2}=30$

Áp dụng công thức Heron ta tính được diện tích tam giác ABC là:

$S=\sqrt{30.(30-15).(30-18).(30-27)}=\sqrt{16200}=90\sqrt{2}$

Mặt khác S = pr (r là bán kính đường tròn nội tiếp tam giác ABC)

Suy ra $r=\frac{S}{p}=\frac{90\sqrt{2}}{30}=3\sqrt{2}$.

Vậy diện tích tam giác ABC là  $90\sqrt{2}$ (đơn vị diện tích) ; bán kính đường tròn nội tiếp tam giác ABC là $3\sqrt{2}$ (đơn vị dộ dài).

b) Do G là trọng tâm tam giác ABC nên G chia tam giác ABC thành ba tam giác GAB, GAC, GBC có diện tích bằng nhau.

Suy ra $S_{GBC}=\frac{S_{ABC}}{3}=\frac{90\sqrt{2}}{3}=30\sqrt{2}$

Vậy diện tích của tam giác GBC là :  $30\sqrt{2}$ (đơn vị diện tích).

Bài 8 trang 73 Toán lớp 10 Tập 1: Cho h_a là đường cao vẽ từ đỉnh A, R là bán kính đường tròn ngoại tiếp tam giác ABC. Chứng minh hệ thức h_a = 2RsinBsinC.

Lời giải:

Trong tam giác ABC, đặt BC = a, AC = b, AB = c, h_a là đường cao vẽ từ đỉnh A, R là bán kính đường tròn ngoại tiếp tam giác ABC.

Ta có diện tích tam giác ABC : S = $\frac{1}{2}a.h_a$  ⇒ $h_a=\frac{2S}{a}$.

Mà  $S=\frac{abc}{4R}\Rightarrow h_a=\frac{2.\frac{abc}{4R}}{a}=\frac{2bc}{4R}=\frac{bc}{2R}$        (1)

Theo định lí sin ta có :   $\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}=2R\Rightarrow b=2R\sin B;\text{ c\hspace{0.17em}=\hspace{0.17em}}2R\sin C$      (2)

Thế (2) vào (1) ta có :

$h_a=\frac{2R\sin B.2R\sin C}{2R}=2R\sin B.\sin C$

Vậy h_a = 2RsinBsinC.

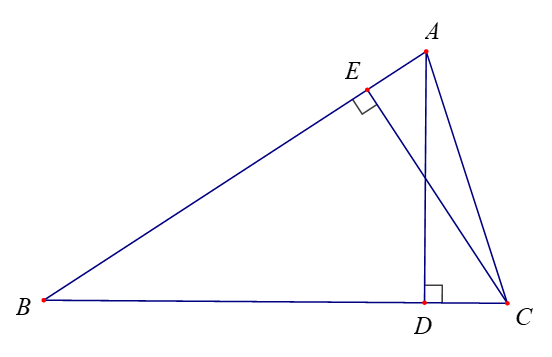
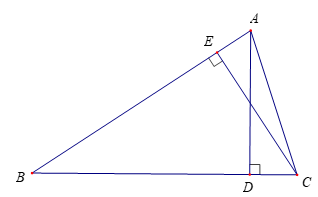
Bài 9 trang 73 Toán lớp 10 Tập 1: Cho tam giác ABC có góc B nhọn, AD và CE là hai đường cao.

a) Chứng minh $\frac{S_{BDE}}{S_{BAC}}=\frac{BD.BE}{BA.BC}$

b) Biết rằng S_ABC = 9S_BDE và DE = $2\sqrt{2}$. Tính cosB và bán kính đường tròn ngoại tiếp tam giác ABC.

Lời giải:

a) Áp dụng công thức tính diện tích tam giác cho hai tam giác BDE và tam giác ABC ta có:

$S_{BDE}=\frac{1}{2}.BD.BE.\sin B$

$S_{ABC}=\frac{1}{2}.BA.BC.\sin B$

Suy ra $\frac{S_{BDE}}{S_{BAC}}=\frac{\frac{1}{2}BD.BE.\sin B}{\frac{1}{2}BA.BC.\sin B}=\frac{BD.BE}{BA.BC}$

Vậy $\frac{S_{BDE}}{S_{BAC}}=\frac{BD.BE}{BA.BC}$

b) Từ S_ABC = 9S_BDE ⇒ $\frac{S_{BDE}}{S_{BAC}}=\frac{BD.BE}{BA.BC}=\frac{1}{9}$

Tam giác BEC vuông tại E có: cosB = $\frac{BE}{BC}$ .

Tam giác ADB vuông tại D có: cosB = $\frac{BD}{AB}$ .

Suy ra cos²B = $\frac{BE}{BC}.\frac{BD}{AB}= \frac{BD.BE}{BA.BC}=\frac{1}{9} \Rightarrow \cos B=\pm \frac{1}{3}$ 

Mặt khác, vì góc B nhọn nên sinB > 0, cosB > 0, do đó: cosB = $\frac{1}{3}$

Mà sin²B + cos²B = 1, suy ra sinB = $\sqrt{1-{\cos }^{2}B}=\sqrt{1-{\left(\frac{1}{3}\right)}^2}=\frac{2\sqrt{2}}{3}$

Xét hai tam giác BDE và tam giác BAC có:

$\frac{BE}{BC}=\frac{BD}{AB}=\frac{1}{3}$  (cùng bằng cosB)

Góc B chung

Suy ra hai tam giác BDE và tam giác BAC đồng dạng theo hệ số tỉ lệ k = $\frac{1}{3}$

⇒ $\frac{DE}{AC}=\frac{1}{3}\Rightarrow AC=3DE=3.2\sqrt{2}=6\sqrt{2}$

Áp dụng định lí sin cho hai tam giác BAC và tam giác BDE ta có:

$\frac{AC}{\sin B}=2R$;  $\frac{DE}{\sin B}=2R\text{'}\Rightarrow R\text{'}=\frac{DE}{2\sin B}=\frac{2\sqrt{2}}{2.\frac{2\sqrt{2}}{3}}=\frac{3}{2}$ (R’ là bán kính đường tròn ngoại tiếp tam giác BDE).

⇒ $\frac{R}{R\text{'}}=\frac{AC}{DE}=\frac{6\sqrt{2}}{2\sqrt{2}}=3$ ⇒ R = 3R' = $3.\frac{3}{2}=\frac{9}{2}$

Vậy cosB = $\frac{1}{3}$; R = $\frac{9}{2}$

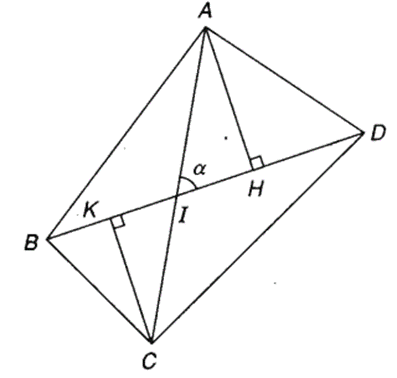
Bài 10 trang 73 Toán lớp 10 Tập 1: Cho tứ giác lồi ABCD có các đường chéo AC = x, BD = y và góc giữa AC và BD bằng α. Gọi S là diện tích của tứ giác ABCD.

a) Chứng minh $S=\frac{1}{2}xy\sin \alpha$

b) Nêu kết quả trong trường hợp AC ⊥ BD.

Lời giải:

a) Ta có S_ABCD = S_ABD + S_CBD.

Vẽ AH và CK vuông góc với BD tại H và K.

Gọi I là giao điểm của hai đường chéo AC và BD.

Ta có : AH = AI.sinα ; CK = CI.sinα.

$S_{ABCD}=\frac{1}{2}AH.BD+\frac{1}{2}CK.BD=\frac{1}{2}BD.(AH+CK)=\frac{1}{2}BD.(AI+IC)\sin \alpha =\frac{1}{2}BD.AC\sin \alpha$

⇒ $S_{ABCD}=\frac{1}{2}x.y\sin \alpha$

b) Nếu AC ⊥ BD thì sinα = sin90° = 1, khi đó $S_{ABCD}=\frac{1}{2}x.y$

Như vậy nếu tứ giác lồi có hai đường chéo vuông góc với nhau thì diện tích của tứ giác đó bằng một nửa tích độ dài của hai đường chéo.

Lời giải bài tập Toán lớp 10 Bài 2: Định lí côsin và định lí sin Chân trời sáng tạo hay khác:

• Giải Toán 10 trang 65

• Giải Toán 10 trang 66

• Giải Toán 10 trang 67

• Giải Toán 10 trang 69

• Giải Toán 10 trang 70

• Giải Toán 10 trang 71

• Giải Toán 10 trang 72