Từ vị trí A, người ta quan sát một cái cây cao mọc vuông góc với mặt đất như hình vẽ. Biết vị trí quan sát cách mặt đất một khoảng AH = 4 m và khoảng cách từ chân đường vuông góc của vị trí
Câu hỏi:
Từ vị trí A, người ta quan sát một cái cây cao mọc vuông góc với mặt đất như hình vẽ.
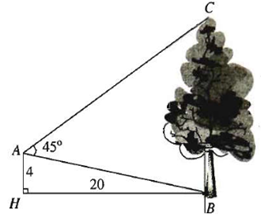
Biết vị trí quan sát cách mặt đất một khoảng AH = 4 m và khoảng cách từ chân đường vuông góc của vị trí quan sát A trên mặt đất tới gốc cây là HB = 20 m, \(\widehat {BAC} = 45^\circ \). Chiều cao của cây gần nhất với giá trị nào sau đây?
A. 17,5 m;
B. 17 m;
C. 16,5 m;
D. 16 m.
Trả lời:
Hướng dẫn giải
Đáp án đúng là: A
Xét ∆ABH vuông tại H có \(\tan \widehat {ABH} = \frac{{AH}}{{HB}} = \frac{4}{{20}} = \frac{1}{5}\).
Suy ra \(\widehat {ABH} \approx 11^\circ 19'\).
Ta có CB ⊥ BH (cái cây vuông góc với mặt đất)
Suy ra \(\widehat {CBH} = 90^\circ \).
Do đó \(\widehat {CBA} + \widehat {ABH} = 90^\circ \)
Vì vậy \(\widehat {CBA} = 90^\circ - \widehat {ABH} \approx 90^\circ - 11^\circ 19' = 78^\circ 41'\).
∆ABC có \(\widehat {CAB} + \widehat {CBA} + \widehat {ACB} = 180^\circ \) (định lí tổng ba góc trong một tam giác)
Suy ra \(\widehat {ACB} = 180^\circ - \left( {\widehat {CAB} + \widehat {CBA}} \right) \approx 180^\circ - \left( {45^\circ + 78^\circ 41'} \right) = 56^\circ 19'\).
∆ABH vuông tại H nên theo định lí Pythagore ta có:
AB2 = AH2 + BH2
= 42 + 202 = 416
Suy ra AB = \(4\sqrt {26} \) (m)
Áp dụng định lí sin cho ∆ABC, ta được \(\frac{{BC}}{{\sin \widehat {BAC}}} = \frac{{AB}}{{\sin \widehat {ACB}}}\)
Suy ra \(\frac{{BC}}{{\sin 45^\circ }} = \frac{{4\sqrt {26} }}{{\sin 56^\circ 19'}}\)
Do đó \(BC = \frac{{4\sqrt {26} .\sin 45^\circ }}{{\sin 56^\circ 19'}} \approx 17,33\) (m).
Giá trị này gần với 17,5 (m)
Vậy ta chọn phương án A.
Xem thêm bài tập trắc nghiệm Toán 10 CTST có lời giải hay khác:
Câu 1:
Cho biết tanα = –3 (0° ≤ α ≤ 180°). Giá trị của \(H = \frac{{6\sin \alpha - 7\cos \alpha }}{{6\cos \alpha + 7\sin \alpha }}\) bằng:
Xem lời giải »
Câu 2:
Cho biết sinα – cosα = \(\frac{1}{{\sqrt 5 }}\)(0° ≤ α, β ≤ 180°). Giá trị của \(E = \sqrt {{{\sin }^4}\alpha + {{\cos }^4}\alpha } \) bằng:
Xem lời giải »
Câu 3:
Cho biết \(2\cos \alpha + \sqrt 2 \sin \alpha = 2\), với 0° < α < 90°. Giá trị của cotα bằng:
Xem lời giải »
Câu 4:
Cho ∆ABC và các khẳng định sau:
(I) b2 – c2 = a(b.cosC – c.cosB);
(II) (b + c)sinA = a(sinB + sinC);
(III) ha = 2R.sinB.sinC;
(IV) S = R.r.(sinA + sinB + sin C);
Số khẳng định đúng là:
Xem lời giải »
Câu 5:
Giả sử CD = h là chiều cao của tháp, trong đó C là chân tháp.
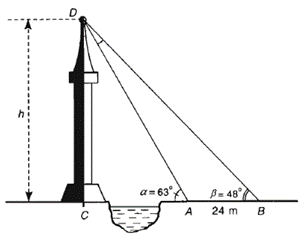
Một người đứng tại vị trí A (\(\widehat {CAD} = 63^\circ ),\) không sang được bờ bên kia để đo chiều cao h của tháp nên chọn thêm một điểm B (ba điểm A, B, C thẳng hàng) cách A một khoảng 24 m và \[\widehat {CBD} = 48^\circ \] để tính toán được chiều cao của tháp. Chiều cao h của tháp gần nhất với:
Xem lời giải »
Câu 6:
Trên nóc một tòa nhà có một cột ăng-ten cao 5 m. Từ vị trí quan sát A cao 7 m so với mặt đất, có thể nhìn thấy đỉnh B và chân C của cột ăng-ten dưới góc 50° và 40° so với phương nằm ngang.
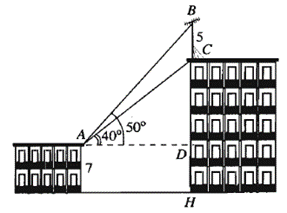
Chiều cao của tòa nhà gần nhất với giá trị nào sau đây?
Xem lời giải »
Câu 7:
Từ hai vị trí A và B của một tòa nhà, người ta quan sát được đỉnh C của ngọn núi. Biết rằng độ cao của tòa nhà là AB = 70 m, phương nhìn AC tạo với phương ngang AH một góc bằng 30°, phương nhìn BC tạo với phương ngang BD một góc bằng 15°30’.
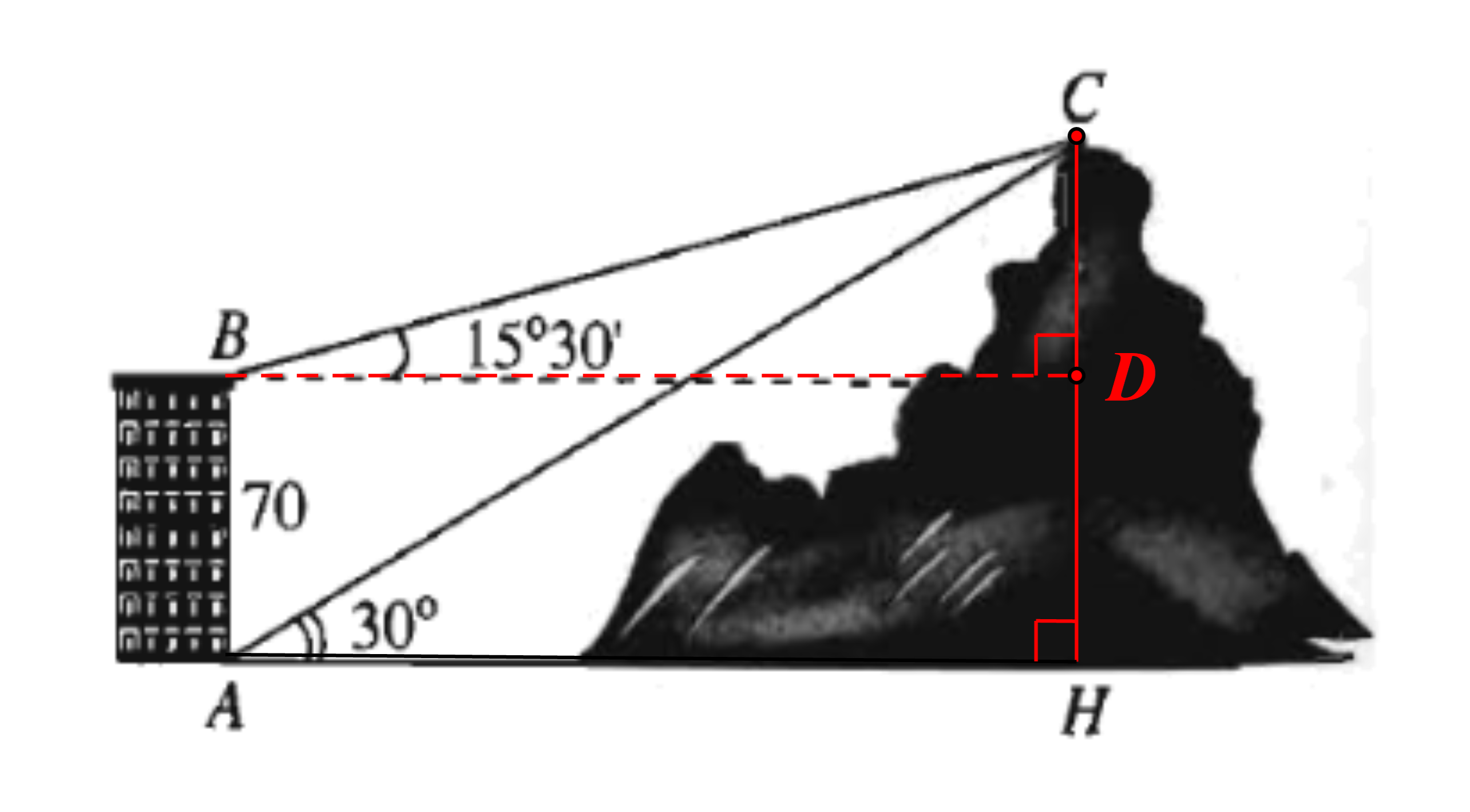
Ngọn núi đó có độ cao so với mặt đất gần nhất với giá trị nào sau đây?
Xem lời giải »





