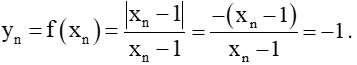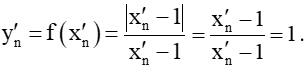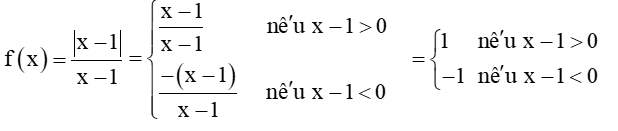HĐ2 trang 113 Toán 11 Tập 1 - Kết nối tri thức

Nhận biết khái niệm giới hạn một bên

Giải Toán 11 Bài 16: Giới hạn của hàm số - Kết nối tri thức

HĐ2 trang 113 Toán 11 Tập 1: Nhận biết khái niệm giới hạn một bên

Cho hàm số .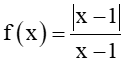

a) Cho $x_n=\frac{n}{n+1}$ và ${x^{\text{'}}}_n=\frac{n+1}{n}$. Tính y_n = f(x_n) và y'_n = f(x'_n).

b) Tìm giới hạn của các dãy số (y_n) và (y'_n).

c) Cho các dãy số (x_n) và (x'_n) bất kì sao cho x_n < 1 < x'_n và x_n ⟶ 1, x'_n ⟶ 1, tính $\underset{n\to +\infty }{\lim }f\left(x_n\right)$ và $\underset{n\to +\infty }{\lim }f\left({x^{\text{'}}}_n\right)$.

Lời giải:

a) Ta có: $x_n=\frac{n}{n+1}<1$ với mọi n $\Rightarrow x_n-1<0$ với mọi n.

Do đó,

Ta cũng có: ${x^{\text{'}}}_n=\frac{n+1}{n}>1$ với mọi n ⇒ x'_n – 1 > 0 với mọi n.

Do đó,

b) Ta có $\underset{n\to +\infty }{\lim }{y}_n=\underset{n\to +\infty }{\lim }\left(-1\right)=-1$; $\underset{n\to +\infty }{\lim }{y^{\text{'}}}_n=\underset{n\to +\infty }{\lim }1=1$.

c) Ta có:

Vì x_n < 1 < x'_n, suy ra x_n – 1 < 0 và x'_n – 1 > 0 với mọi n.

Do đó, f(x_n) = – 1 và f(x'_n) = 1.

Vậy $\underset{n\to +\infty }{\lim }f\left(x_n\right)$= – 1 và $\underset{n\to +\infty }{\lim }f\left({x^{\text{'}}}_n\right)$= 1.

Lời giải bài tập Toán 11 Bài 16: Giới hạn của hàm số hay, chi tiết khác:

• Mở đầu trang 111 Toán 11 Tập 1: Trong Thuyết tương đối của Einstein, khối lượng của vật chuyển động với vận tốc v....

• HĐ1 trang 111 Toán 11 Tập 1: Nhận biết khái niệm giới hạn tại một điểm ....

• Luyện tập 1 trang 113 Toán 11 Tập 1: Tính $\underset{x\to 1}{\lim }\frac{x-1}{\sqrt{x}-1}$ ....

• Luyện tập 2 trang 113 Toán 11 Tập 1: Cho hàm số ....

• HĐ3 trang 114 Toán 11 Tập 1: Nhận biết khái niệm giới hạn tại vô cực ....

• Luyện tập 3 trang 115 Toán 11 Tập 1: Tính $\underset{x\to +\infty }{\lim }\frac{\sqrt{x^2+2}}{x+1}$. ....

• Vận dụng trang 115 Toán 11 Tập 1: Cho tam giác OAB với A = (a; 0) và B = (0; 1) như Hình 5.5 ....

• HĐ4 trang 115 Toán 11 Tập 1: Nhận biết khái niệm giới hạn vô cực ....

• HĐ5 trang 116 Toán 11 Tập 1: Cho hàm số $f\left(x\right)=\frac{1}{x-1}$ ....

• Luyện tập 4 trang 116 Toán 11 Tập 1: Tính các giới hạn sau: ....

• Luyện tập 5 trang 118 Toán 11 Tập 1: Tính $\underset{x\to 2^{+}}{\lim }\frac{2x-1}{x-2}$ ....

• Bài 5.7 trang 118 Toán 11 Tập 1: Cho hai hàm số $f\left(x\right)=\frac{x^2-1}{x-1}$ và g(x) = x + 1 ....

• Bài 5.8 trang 118 Toán 11 Tập 1: Tính các giới hạn sau: ....

• Bài 5.9 trang 118 Toán 11 Tập 1: Cho hàm số ....

• Bài 5.10 trang 118 Toán 11 Tập 1: Tính các giới hạn một bên: ....

• Bài 5.11 trang 118 Toán 11 Tập 1: Cho hàm số g(x) ....

• Bài 5.12 trang 118 Toán 11 Tập 1: Tính các giới hạn sau: a) $\underset{x\to +\infty }{\lim }\frac{1-2x}{\sqrt{x^2+1}}$ ....

• Bài 5.13 trang 118 Toán 11 Tập 1: Cho hàm số $f\left(x\right)=\frac{2}{\left(x-1\right)\left(x-2\right)}$ ....