HĐ3 trang 33 Toán 11 Tập 2 - Kết nối tri thức

Giải Toán 11 Bài 23: Đường thẳng vuông góc với mặt phẳng - Kết nối tri thức

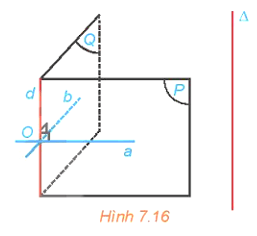
HĐ3 trang 33 Toán 11 Tập 2: Cho điểm O và đường thẳng ∆ không đi qua O. Gọi  d là đường thẳng đi qua O và song song với ∆. Xét hai mặt phẳng phân biệt tuỳ ý (P) và (Q) cùng chứa d. Trong các mặt phẳng (P), (Q) tương ứng kẻ các đường thẳng a, b cùng đi qua O và vuông góc với d (H.7.16). Giải thích vì sao mp(a, b) đi qua O và vuông góc với ∆.

Lời giải:

Ta có (P) = mp(d, a) và (Q) = mp(d, b).

Do (P) và (Q) là hai mặt phẳng phân biệt nên a và b là hai đường thẳng phân biệt.

Do $\left.\begin{array}{l}d\perp a\\ d\text{\hspace{0.17em}//}\Delta \end{array}\right\}\Rightarrow a\perp \Delta$ hay (D, a) = (d, a) = 90°.

Do $\left.\begin{array}{l}d\perp b\\ d\text{\hspace{0.17em}//\hspace{0.17em}}\Delta \end{array}\right\}\Rightarrow b\perp \Delta$ hay (D, b) = (d, b) = 90°.

Vậy D vuông góc với a và b và a, b đi qua O nên D ⊥ mp(a, b).

Lời giải bài tập Toán 11 Bài 23: Đường thẳng vuông góc với mặt phẳng hay, chi tiết khác:

• HĐ1 trang 31 Toán 11 Tập 2: Đối với cánh cửa như trong Hình 7.10, khi đóng – mở cánh cửa ....

• Câu hỏi trang 32 Toán 11 Tập 2: Nếu đường thẳng ∆ và mặt phẳng (P) vuông góc với nhau thì chúng có cắt nhau hay không? ....

• HĐ2 trang 32 Toán 11 Tập 2: Gấp tấm bìa cứng hình chữ nhật sao cho nếp gấp chia tấm bìa thành hai hình chữ nhật ....

• Câu hỏi trang 32 Toán 11 Tập 2: Nếu một đường thẳng vuông góc với hai cạnh của một tam giác thì đường thẳng ....

• Luyện tập 1 trang 32 Toán 11 Tập 2: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O ....

• Vận dụng trang 33 Toán 11 Tập 2: Khi làm cột treo quần áo, ta có thể tạo hai thanh đế thẳng đặt dưới sàn nhà ....

• HĐ4 trang 34 Toán 11 Tập 2: Cho mặt phẳng (P) và điểm O. Trong mặt phẳng (P), lấy hai đường thẳng cắt nhau a ....

• Luyện tập 2 trang 34 Toán 11 Tập 2: Cho ba điểm phân biệt A, B, C sao cho các đường thẳng AB và AC cùng vuông góc ....

• HĐ5 trang 34 Toán 11 Tập 2: Cho đường thẳng a vuông góc với mặt phẳng (P) và song song với đường thẳng b ....

• HĐ6 trang 34 Toán 11 Tập 2: Cho hai đường thẳng phân biệt a và b cùng vuông góc với mặt phẳng (P) ....

• HĐ7 trang 35 Toán 11 Tập 2: Cho hai mặt phẳng (P) và (Q) song song với nhau và đường thẳng ∆ vuông góc với (P) ....

• HĐ8 trang 35 Toán 11 Tập 2: Cho hai mặt phẳng (P) và (Q) cùng vuông góc với đường thẳng ∆ ....

• Luyện tập 3 trang 35 Toán 11 Tập 2: Một chiếc bàn có các chân cùng vuông góc với mặt phẳng chứa mặt bàn và mặt phẳng ....

• HĐ9 trang 35 Toán 11 Tập 2: Cho đường thẳng a song song với mặt phẳng (P) và đường thẳng ∆ vuông góc ....

• HĐ10 trang 36 Toán 11 Tập 2: Cho đường thẳng a và mặt phẳng (P) cùng vuông góc với một đường thẳng ∆ ....

• Luyện tập 4 trang 36 Toán 11 Tập 2: : Cho hình chóp S.ABCD có đáy ABCD là một hình vuông, SA ⊥ (ABCD) ....

• Bài 7.5 trang 36 Toán 11 Tập 2: Cho hình chóp S.ABC có đáy là tam giác cân tại A và $SA\perp \left(ABC\right)$ ....

• Bài 7.6 trang 36 Toán 11 Tập 2: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật và $SA\perp \left(ABCD\right)$ ....

• Bài 7.7 trang 36 Toán 11 Tập 2: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật và $SA\perp \left(ABCD\right)$. Gọi M, N tương ứng là hình chiếu của A trên SB ....

• Bài 7.8 trang 36 Toán 11 Tập 2: Bạn Vinh thả quả dọi chìm vào thùng nước ....

• Bài 7.9 trang 36 Toán 11 Tập 2: Một cột bóng rổ được dựng trên một sân phẳng ....