HĐ4 trang 18 Toán 11 Tập 2 - Kết nối tri thức
Giải Toán 11 Bài 20: Hàm số mũ và hàm số lôgarit - Kết nối tri thức
HĐ4 trang 18 Toán 11 Tập 2: Nhận dạng đồ thị và tính chất của hàm số lôgarit
Cho hàm số lôgarit y = log2x.
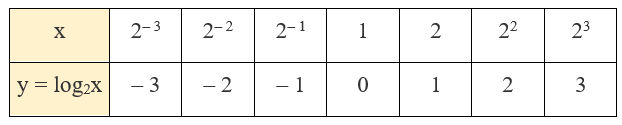
a) Hoàn thành bảng giá trị sau:
b) Trong mặt phẳng toạ độ Oxy, biểu diễn các điểm (x; y) trong bảng giá trị ở câu a. Bằng cách làm tương tự, lấy nhiều điểm (x; log2x) và nối lại ta được đồ thị của hàm số y = log2x.
c) Từ đồ thị đã vẽ ở câu b, hãy kết luận về tập giá trị và tính chất biến thiên của hàm số y = log2x.
Lời giải:
a) Ta có log22– 3 = – 3; log22– 2 = – 2; log22– 1 = – 1; log21 = 0; log22 = 1; log222 = 2; log223 = 3. Vậy ta hoàn thành được bảng đã cho như sau:
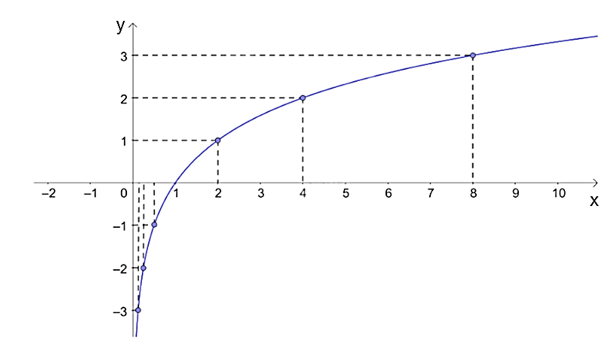
b) Trên mặt phẳng tọa độ Oxy, ta biểu diễn các điểm (x; y) ở câu a và lấy thêm nhiều điểm (x; log2x) với x > 0, nối lại ta được đồ thị của hàm số y = log2x như sau:
c) Từ đồ thị đã vẽ ở câu b, nhận thấy hàm số y = log2x:
+ Có tập giá trị là ℝ;
+ Đồng biến trên (0; + ∞).
Lời giải bài tập Toán 11 Bài 20: Hàm số mũ và hàm số lôgarit hay, chi tiết khác:
HĐ2 trang 16 Toán 11 Tập 2: Nhận dạng đồ thị và tính chất của hàm số mũ Cho hàm số mũ y = 2x ....
Câu hỏi trang 18 Toán 11 Tập 2: Trong các hàm số sau, những hàm số nào là hàm số lôgarit ....