Bài 11 trang 136 Toán 8 Tập 2 | Kết nối tri thức Giải Toán 8

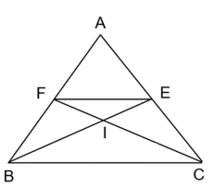
Cho tam giác ABC cân tại đỉnh A. Hai đường phân giác BE và CF của tam giác ABC cắt nhau tại điểm I.

Giải Toán 8 Bài tập ôn tập cuối năm - Kết nối tri thức

Bài 11 trang 136 Toán 8 Tập 2: Cho tam giác ABC cân tại đỉnh A. Hai đường phân giác BE và CF của tam giác ABC cắt nhau tại điểm I.

a) Chứng minh ΔBIC ∽ ΔEIF.

b) Chứng minh FB² = FI ∙ FC.

c) Cho biết AB = 6 cm, BC = 3 cm. Tính EF.

Lời giải:

Bài 11 trang 136 Toán 8 Tập 2 | Kết nối tri thức Giải Toán

a) Do BE là đường phân giác của góc B nên ta có $\frac{E A}{E C} = \frac{B A}{B C}$ (1).

Tương tự với đường phân giác CF ta có $\frac{F A}{F B} = \frac{C A}{C B}$ (2).

Do tam giác ABC cân tại A nên BA = AC, kết hợp với (1) và (2) suy ra $\frac{E A}{E C} = \frac{F A}{F B}$

Do đó, theo định lí Thalès đảo ta có EF // BC. Suy ra ∆BIC ∽ ∆EIF.

b) Ta có $\hat{A B E} = \frac{1}{2} \hat{A B C}$ (do BE là đường phân giác của góc B)

$\hat{B C F} = \frac{1}{2} \hat{A C B}$ (do CF là đường phân giác của góc C)

$\hat{A B C} = \hat{A C B}$ (do tam giác ABC cân tại A).

Do đó, $\hat{A B E} = \hat{B C F}$ .

Hai tam giác BFI và CFB có góc F chung và $\hat{A B E} = \hat{B C F}$ (chứng minh trên).

Do đó ∆BFI ∽ ∆CFB (g.g).

Suy ra $\frac{F B}{F C} = \frac{F I}{F B} \Rightarrow F B^{2} = F I \cdot F C$ (đpcm).

c) Theo câu a) ta có $\frac{F A}{F B} = \frac{C A}{C B}$ hay $\frac{F B}{F A} = \frac{B C}{B A}$ .

Ta có EF // BC (chứng minh trên), do đó

$\frac{B C}{E F} = \frac{A B}{A F} \Rightarrow \frac{B C}{E F} = \frac{(A F + F B)}{A F}$ $= 1 + \frac{F B}{F A} = 1 + \frac{B C}{B A} = 1 + \frac{3}{6} = \frac{3}{2}$ .

Từ đó ta có $\frac{3}{F E} = \frac{3}{2} \Rightarrow F E = 2$ cm.

Lời giải bài tập Toán 8 Bài tập ôn tập cuối năm hay, chi tiết khác:

Xem thêm lời giải bài tập Toán 8 Kết nối tri thức hay, chi tiết khác:

❮ Bài trước Bài sau ❯