Bài 8 trang 136 Toán 8 Tập 2 | Kết nối tri thức Giải Toán 8

❮ Bài trước Bài sau ❯

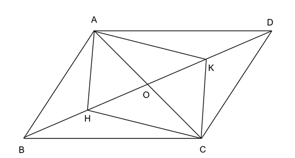
Cho hình bình hành ABCD, O là giao điểm của hai đường chéo AC và BD. Gọi H là trung điểm của OB, K là trung điểm của OD.

Giải Toán 8 Bài tập ôn tập cuối năm - Kết nối tri thức

Bài 8 trang 136 Toán 8 Tập 2: Cho hình bình hành ABCD, O là giao điểm của hai đường chéo AC và BD. Gọi H là trung điểm của OB, K là trung điểm của OD.

a) Hỏi tứ giác AHCK là hình gì?

b) Hình bình hành ABCD phải thỏa mãn điều kiện gì để tứ giác AHCK là:

– một hình thoi?

– một hình chữ nhật?

– một hình vuông?

Lời giải:

Bài 8 trang 136 Toán 8 Tập 2 | Kết nối tri thức Giải Toán

a) Vì O là giao điểm của hai đường chéo AC và BD nên O là trung điểm của AC và BD.

Ta có H là trung điểm của BO suy ra HB = HO = $\frac{1}{2} O B$ ;

K là trung điểm của OD nên OK = KD = $\frac{1}{2} O D$ .

Mà OB = OD (O là trung điểm của BD) nên OK = OH, suy ra O là trung điểm của HK.

Tứ giác AHCK có O là trung điểm của hai đường chéo AC và HK.

Suy ra tứ giác AHCK là hình bình hành.

+ Muốn tứ giác AHCK là hình thoi ta cần thêm điều kiện hai đường chéo AC và HK vuông góc với nhau, cũng có nghĩa là hai đường chéo của hình bình hành ABCD vuông góc với nhau, vậy để tứ giác AHCK là hình thoi thì tứ giác ABCD là hình thoi.

+ Muốn tứ giác AHCK là hình chữ nhật, ta cần thêm điều kiện hai đường chéo AC và HK bằng nhau, cũng có nghĩa là đường chéo AC của hình bình hành ABCD bằng nửa đường chéo BD (Do H, K lần lượt là trung điểm của OB và OD).

Vậy để tứ giác AHCK là hình chữ nhật điều kiện là: ABCD có đường chéo BD dài gấp hai lần đường chéo AC.

+ Tứ giác AHCK là hình vuông khi nó vừa là hình thoi, vừa là hình chữ nhật. Muốn vậy, thêm kết quả hai câu trên, tứ giác ABCD thỏa mãn điều kiện vừa là hình thoi và vừa có đường chéo BD dài gấp hai lần đường chéo AC.

Lời giải bài tập Toán 8 Bài tập ôn tập cuối năm hay, chi tiết khác:

Xem thêm lời giải bài tập Toán 8 Kết nối tri thức hay, chi tiết khác:

❮ Bài trước Bài sau ❯