Bài 1 trang 97 Toán 9 Tập 1 Chân trời sáng tạo

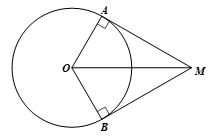
Cho đường tròn (O; 5 cm) và điểm M sao cho OM = 10 cm. Qua M vẽ hai tiếp tuyến với đường tròn tại A và B. Tính số đo góc ở tâm được tạo bởi hai tia OA và OB.

Giải Toán 9 Bài 3: Góc ở tâm, góc nội tiếp - Chân trời sáng tạo

Bài 1 trang 97 Toán 9 Tập 1: Cho đường tròn (O; 5 cm) và điểm M sao cho OM = 10 cm. Qua M vẽ hai tiếp tuyến với đường tròn tại A và B. Tính số đo góc ở tâm được tạo bởi hai tia OA và OB.

Lời giải:

Xét đường tròn (O; 5 cm), ta có: MA, MB lần lượt là tiếp tuyến tại A, B của (O) nên MA ⊥ OA tại A (tính chất tiếp tuyến) và OM là tia phân giác của $\widehat{AOB}$(tính chất hai tiếp tuyến cắt nhau).

Xét ∆OAM vuông tại A, ta có: $\cos \widehat{AOM}=\frac{OA}{OM}=\frac{5}{10}=\frac{1}{2}.$

Suy ra $\stackrel{⏜}{AOM} ={60}^0$

Do đó $\widehat{AOB}=2\widehat{AOM}=2\cdot 60°=120°$(do OM là tia phân giác của $\widehat{AOB}$

Vậy số đo góc ở tâm được tạo bởi hai tia OA và OB là $\widehat{AOB}$ = 120⁰

Lời giải bài tập Toán 9 Bài 3: Góc ở tâm, góc nội tiếp hay, chi tiết khác:

• Khởi động trang 90 Toán 9 Tập 1: Hình ngôi sao năm cánh trong Hình a được vẽ lại như Hình b. Phần tô màu xanh trên đường tròn từ điểm A đến điểm B ....

• Khám phá 1 trang 90 Toán 9 Tập 1: Cho hai điểm A, B trên đường tròn (O; R). Nêu nhận xét về đỉnh và cạnh của $\widehat{AOB}.$ ....

• Thực hành 1 trang 90 Toán 9 Tập 1: Tính số đo góc ở tâm $\widehat{EOA}$ và $\widehat{AOB}$ trong Hình 3. Biết AC và BE là hai đường kính của đường tròn (O) ....

• Vận dụng 1 trang 91 Toán 9 Tập 1: Tính số đo góc ở tâm được tạo thành khi kim giờ quay ....

• Khám phá 2 trang 91 Toán 9 Tập 1: Vẽ vào vở đường tròn (O) và hai điểm A, B nằm trên (O). Dùng bút chì khác màu tô hai phần ....

• Khám phá 3 trang 91 Toán 9 Tập 1: Cho OA và OB là hai bán kính vuông góc với nhau của đường tròn (O), C là điểm trên cung nhỏ AB (Hình 7) ....

• Thực hành 2 trang 92 Toán 9 Tập 1: Cho đường tròn (O) có hai đường kính AB và CD vuông góc với nhau (Hình 9). ....

• Vận dụng 2 trang 92 Toán 9 Tập 1: Xác định số đo cung AB trong hình ngôi sao năm cánh (Hình 10) ....

• Khám phá 4 trang 92 Toán 9 Tập 1: Trên đường tròn (O), vẽ hai cung nhỏ $\stackrel{⏜}{AB},\stackrel{⏜}{BC}$ sao cho $\widehat{AOB}=18°,\widehat{BOC}=32°$ ....

• Thực hành 3 trang 93 Toán 9 Tập 1: Trên cung AB có số đo 90° của đường tròn (O), lấy điểm M sao cho cung AM có số đo 15° ....

• Vận dụng 3 trang 93 Toán 9 Tập 1: Bạn Hùng làm một cái diều với thân diều là hình tứ giác SAOB sao cho OS là đường phân giá ....

• Khám phá 5 trang 93 Toán 9 Tập 1: Quan sát Hình 13. Hãy cho biết trong các góc $\widehat{APB},\widehat{AOB},\widehat{AMB},\widehat{AQB},$ góc nào có đỉnh nằm trên đường tròn (O) ....

• Thực hành 4 trang 93 Toán 9 Tập 1: Cho tam giác đều MNP có ba đỉnh nằm trên đường tròn (I). Hãy chỉ ra các góc nội tiếp của đường tròn (I) ....

• Vận dụng 4 trang 93 Toán 9 Tập 1: Cho hai điểm E và F nằm trên đường tròn (O). Có bao nhiêu góc nội tiếp chắn cung EF? ....

• Khám phá 6 trang 94 Toán 9 Tập 1: Quan sát Hình 15. Ta có góc nội tiếp $\widehat{AMB}$ chắn cung AB trên đường tròn (O). Cho biết $\widehat{AOB}=60°.$ ....

• Thực hành 5 trang 96 Toán 9 Tập 1: Cho ba điểm A, B, C nằm trên đường tròn (O) sao cho $\widehat{AOB}=50°,$ ....

• Vận dụng 5 trang 96 Toán 9 Tập 1: Một huấn luyện viên cho cầu thủ tập sút bóng vào cầu môn MN (Hình 20) ....

• Bài 2 trang 97 Toán 9 Tập 1: Cho tam giác đều ABC. Vẽ nửa đường tròn đường kính BC cắt cạnh AB và AC lần lượt tại D và E ....

• Bài 3 trang 97 Toán 9 Tập 1: Dây cung AB chia đường tròn (O) thành hai cung. Cung lớn có số đo bằng ba lần cung nhỏ ....

• Bài 4 trang 97 Toán 9 Tập 1: Kim giờ và kim phút của đồng hồ tạo thành một góc ở tâm có số đo là bao nhiêu vào những thời điểm sau? ....

• Bài 5 trang 97 Toán 9 Tập 1: Cho hai đường tròn đồng tâm (O; R) và $\left(O;\frac{R\sqrt{3}}{2}\right).$ Một tiếp tuyến của đường tròn nhỏ cắt đường tròn lớn tại hai điểm A và B ....

• Bài 6 trang 97 Toán 9 Tập 1: Xác định số đo các cung $\stackrel{⏜}{AB},\stackrel{⏜}{BC},\stackrel{⏜}{CA}$ trong mỗi hình vẽ sau. ....

• Bài 7 trang 97 Toán 9 Tập 1: Cho đường tròn (O) có hai đường kính AB, CD vuông góc với nhau. Lấy một điểm M trên cung nhỏ AC ....